レンダラー開発のための測光学覚書Vol.2　レイトレースのための基本的な物理量からレンダリング方程式まで

　どうも、前回に引き続き、『レンダラー開発のための測光学覚書』シリーズ第2弾です。前回は立体角についての数学の話だったので、今回からは物理の話に入っていきましょう。

基本的な物理量
マテリアルの決定
レンダリング方程式
最後に
- 参考文献

基本的な物理量

放射束

　光とは粒子であり、波である。これが今の物理の定説です。しかし未だに謎が多く、光とは何かというのは完璧に答えることはできません。しかし、光は私たちに世界を知覚させることができる、とても身近な存在ですよね。ゆえに経験からいろんなことがわかります。例えば、虫眼鏡で黒い紙に光を1点に集中させれば火が出るように、光はエネルギーを持っています。ここで紹介する「放射束」は単位時間あたりの光のエネルギーという定義で、測光の分野では最も基本的な物理量です。

$\displaystyle \begin{align} \Phi = \frac{dQ}{dt} \end{align}$

ここで、 $Q$ は光のエネルギー、 $t$ は時間です。

放射照度

単位面積当たりの放射束を放射照度といいます。

$\displaystyle \begin{align} E(x)=\frac{d\Phi}{dA} \end{align}$

放射強度

ここで、前回の内容である、立体角の概念を導入します。ラジアンの立体版でしたね。忘れてしまった方はこちらをどうぞ。
drumath.hatenablog.com
放射強度は単位立体角当たりの放射束として与えられる物理量です。

$\displaystyle \begin{align} I(\vec{\omega})=\frac{d\Phi}{d\vec{\omega}} \end{align}$

ですので、逆に半球について積分してやれば、放射束が求められます。

$\displaystyle \begin{align} \Phi = \int_\Omega I(\vec{\omega}) d\vec{\omega} \end{align}$

放射輝度

　放射輝度は、単位投影面積、単位立体角あたりの放射束として定義されます。先に式を出すと、

$\displaystyle \begin{align} L(x, \vec{\omega})=\frac{d^2\Phi}{\cos \theta dAd\vec{\omega}} \end{align}$

$\cos \theta$ がいきなり出てきましたが、これは定義が単位面積ではなく、「単位投影面積」ということに起因します。
例えば、下の図のように、光が地面に向かって $\theta$ の角度で入射しているとしましょう。
f:id:drumath:20180228002606p:plain

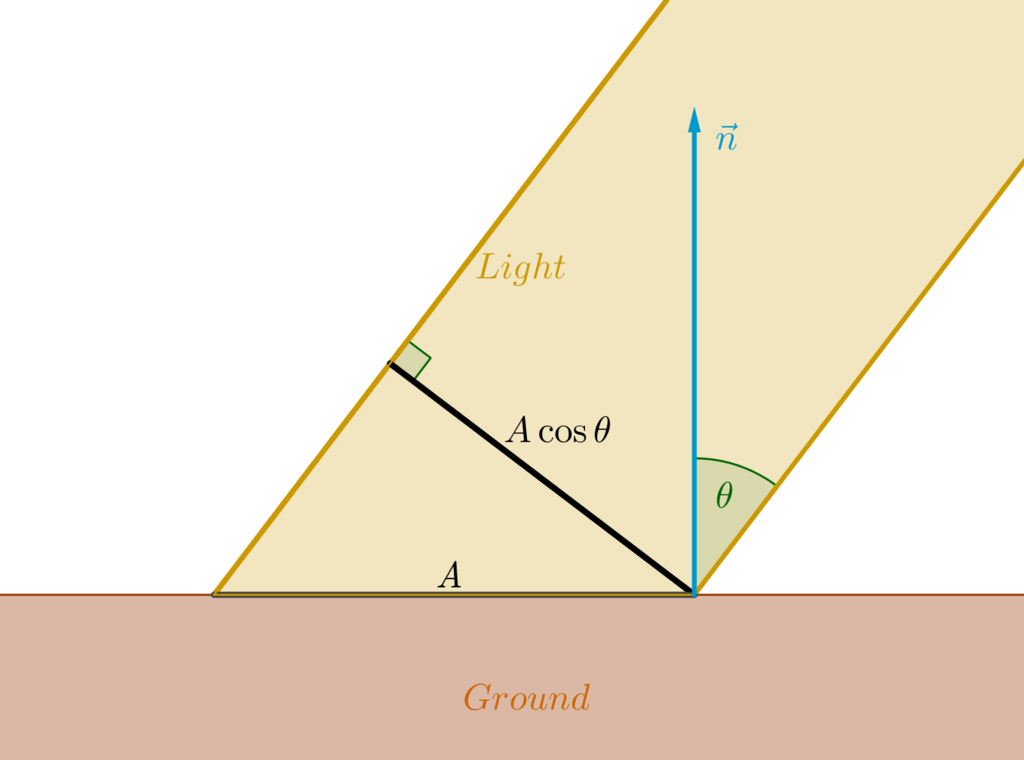
このとき、光が当たっている面積を $A$ とします。このときの放射照度は $\displaystyle E=\frac{\Phi}{A}$ ですね。
ここで、光の進行方向に垂直な面を考えます。すると、その面と光が当たっている面積は、図に示した通り、 $A\cos \theta$ となります。これを、投影面積といいます。
放射輝度は積分すれば、いろんな物理量が導けるので、シミュレーションでは大変重宝します。例えば放射束を出したい時には

$\displaystyle \begin{align} \Phi = \int_A \int_\Omega L(x,\vec{\omega})(\vec{n} \cdot \vec{\omega})d\vec{\omega}dx \end{align}$

上の式では、地面に対する法線ベクトルの単位ベクトルと、入射ベクトルの単位ベクトルの内積を取ることで入射角を求めることができます。この $(\vec{n} \cdot \vec{\omega})$ の項をコサイン項と呼びます。

マテリアルの決定

　ここまで光について見てきました。ここでは実際にレンダリングするとき、もう一つ重要な「どんな材質に光が当たったか」を決めるための関数をご紹介します。

BSSRDF（英：bidirectional scattering surface reflectance distribution function、日：双方向散乱面反射率分布関数）

　光が物質の表面に当たったら、入射角と同じ大きさの反射角で反射し、屈折の法則に従って屈折することは高校生、いや中学生で習いました。しかし現実はそんなに甘くありません。なぜなら完全に平らな面など存在しないからです。実際にはすごく小さな凸凹があって、その凸凹に当たって光はあらゆる方向に反射していきます。これを散乱というのでしたね。また、光はどの物質でも通過します。つまり物質の表面で屈折した光はそのうち物質中で反射して出てくるかもしれないし、反射を繰り返して物質を通過するかもしれないのです。このように物質を通過した光が反射して出ていくことを「表面下散乱」といいます。このように表面化散乱の様子を示す関数が、BSSRDFと呼ばれる関数です。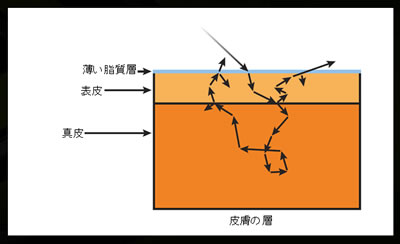

f:id:drumath:20180228153043p:plain — https://news.mynavi.jp/article/graphics-59/　から引用

上の画像からもわかる通り、人の肌の質感などのレンダリングではこの技術が用いられます。しかし、ちょっと複雑ですね。なので普通はBSSRDFを簡略化したBSDFを用います。

BRDF（英：bidirectional reflectance distribution function、日：双方向反射率分布関数）

　BRDFはBSSRDFを簡略化したモデルです。正確に言うと、BSSRDFの簡略版は、BRDFとBTDFを足しあさせたBSDFというモデルなのですが、拡散反射や鏡面反射だけのモデルの場合、BRDFで事足りるということなんだと思います。BRDFは入射位置からでる反射光をモデル化したもので、先ほどの表面下散乱を考えないもので、入射光による放射照度と反射光による放射輝度の比で与えられます。
ここで、式の中の物理量に以下のものを使います。（なんか今更な感じもしますが）

物理量	意味
$\Phi$	放射束
$E$	放射照度
$L$	放射輝度
$f_{r}$	BRDF
$\theta_{i}$	入射角
$\vec{\omega}$	入射光、及び反射光の方向
$\vec{n}$	入射面に対する法線

添え字の $i$ や $r$ はそれぞれ入射光関係(incidence)、反射光関係(reflectance)という意味です。

$\displaystyle \begin{align} BRDF: f_{r} (x, \vec { \omega }_{i}, \vec{\omega}_{r}) &= \frac{dL_{r}(x,\vec{\omega}_{r})}{dE_{i}(x, \vec{\omega}_{i})} \\\ &= \frac{dL_{r}(x, \vec{\omega}_{r})}{L_{i}(x, \vec{\omega}_{i})(\vec{n} \cdot \vec{\omega}_{i})d\vec{\omega}_{i}} \end{align}$

さて式変形についての説明ですが、

$\displaystyle \begin{align} L_{i}(x, \vec{\omega}_{i}) = \frac{d^{2}\Phi}{\cos \theta_{i} dAd\vec{\omega}_{i}} = \frac{dE(x, \vec{\omega}_{i})}{(\vec{n} \cdot \vec{\omega}_{i})d\vec{\omega}_{i}} \end{align}$

となるためですね。

BRDFの意味（高校生なりの解釈）

　私は最初BRDFの式を見て、なんでこうなるんだかわかりませんでしたw　というのも、なぜ放射照度と放射輝度という二つの違う量の比で表すのかが意味不明でした。しかもこんなに複雑な式で、さも微積させる気しかないような雰囲気ですよね。頭の中ではグラサンかけてる厳ついおっさんが突然出てきたみたいなイメージでした。絡みづらいわ。
しかし、BRDFもこんな風に変形すれば、目的は一目瞭然です。

$\displaystyle \begin{align} dL_{r} ( x, \vec { \omega }_{r} ) &= f_{r} ( x, \vec { \omega }_{i}, \vec{\omega}_{r} ) L_{i} (x, \vec { \omega }_{i}) (\vec{n} \cdot \vec { \omega }_{i}) d \vec { \omega }_{i} \\\ \Leftrightarrow L_{r} ( x, \vec { \omega }_{r} ) &= \int_{\Omega} f_{r} ( x, \vec { \omega }_{i}, \vec{\omega}_{r} ) L_{i} (x, \vec { \omega }_{i}) (\vec{n} \cdot \vec { \omega }_{i}) d \vec { \omega }_{i} \tag{1} \end{align}$

つまり何が言いたいかというと、BRDFなんてものは関数というよりもよりも、係数みたいなもんじゃないのか。
このようにすると、後述するレンダリング方程式とほぼ形は一緒です。つまり、いま私たちが求めたいのは放射輝度である。前述のとおり放射輝度さえわかればほかの物理量は積分すれば求まりますからね。だから普通はBRDFを求めよう、なんてことはしないんじゃないかな。
もう一回式(1)を見てみましょう。

$\displaystyle \begin{align} L_{r} ( x, \vec { \omega }_{r} ) &= \int_{\Omega} f_{r} ( x, \vec { \omega }_{i}, \vec{\omega}_{r} ) L_{i} (x, \vec { \omega }_{i}) (\vec{n} \cdot \vec { \omega }_{i}) d \vec { \omega }_{i} \tag{1} \end{align}$

目的は $L_{r}$ を求めることでした。被積分関数を見てみると、3つの項があります。左から順に、BRDF、入射光の放射輝度、コサイン項です。反射光の放射輝度を求めるのには、入射光の放射輝度が必要だということは、納得がいくと思います。またコサイン項があることによって放射輝度が一緒でも、入射角によって反射光の放射輝度が違うことも読み取れます。だから、BRDFというのは、入射光がどれだけ変化するかを表しているだけなのです。ここまでよろしいでしょうか。
半球で積分をしている意味は、面に対して、あらゆる方向から入射してくる光の和という意味ですね。このおかげで、グローバルイルミネーションが実現できます。

レンダリング方程式

さて、ついにレンダリング方程式です。とはいえ、先ほどの内容がわかっていれば余裕です。ようは出ていく放射輝度を求める方程式です。
出射する光というのは、表面から放射される光と反射される光の和で求まります。これは感覚的ですね。つまり、

$L_{r}$	反射光(reflected)の放射輝度
$L_{e}$	放射光(emitted)の放射輝度
$L_{o}$	出射光(outgoing)の放射輝度

とすれば、求める $L_{o}$ は

$\displaystyle \begin{align} L_{o} = L_{e} + L_{r} \end{align}$

となります。また、式(1)より

$\displaystyle \begin{align} L_{o}(x, \vec{\omega}_{r}) = L_{e}(x, \vec{\omega}_{r}) + \int_{\Omega} f_{r} ( x, \vec { \omega }_{i}, \vec{\omega}_{r} ) L_{i} (x, \vec { \omega }_{i}) (\vec{n} \cdot \vec { \omega }_{i}) d \vec { \omega }_{i} \end{align}$

と書き換えられます。お疲れさまでした、レンダリング方程式の出来上がりです！

最後に

ここまで学習するのにはとても時間がかかりました。しかし、レンダリングの原理が少しわかったような気がして、自信が付きました。既存のレンダラーなど見ていると、いつもは何気なく見ている言葉も、「これ知ってる！」ってなってなんだか楽しいですw　BlenderのCyclesレンダラーも、マテリアルの名前は「～～BSDF」という風になってますけど、材質決定の関数だなんて思いませんでした。これからも頻度は高くないかもしれないけど、このシリーズは続けていこうと思います。最後まで見てくださり、ありがとうございました。

参考文献

qiita.com
↑いつもお世話になっています。より詳しい内容が知りたい方はこのリンクへ飛んでみてください。
raytracing.hatenablog.com
↑教育用のレンダラーを作ってくださっています。日本語のコメントがあるって素敵
qiita.com
↑こちらもわかりやすく解説してくださっています。