レンダラー開発のための測光学覚書Vol.3　ランバート反射BRDF

　レン覚（レンダラー開発のための測光学覚書）です！前回の投稿からだいぶ時間がたってしまったこともあり、自分でも記事を読み返したり、勉強しなおしたりしてました。
そして、とうとうレンダラーの開発をはじめたので、備忘録として学んだことをどんどん投稿しようと思います。今回は前回説明した「BRDF」について理解を深めていこうと思います。読みきりサイズなので、是非最後までお付き合いください。

ランバート反射について
ランバート反射のBRDFを求める
おわりに
- 参考
- 7/5追記

ランバート反射について

　さて、今回のテーマとなっている「ランバート反射」とは何かについて、最初に説明しようと思います。ランバート反射は拡散反射の一種で、いうなれば「理想的な拡散反射」です。どういう意味かというと、

光の入射角度にかかわらず、出射光は全ての方向に均一に反射されます。反射面の見た目の明るさ(輝度)はどの方向から見ても一定です。
http://www.systems-eng.co.jp/column/column03.html

らしいです。放射輝度の分布を図で示すとこんな感じです。
f:id:drumath:20180704210330p:plain

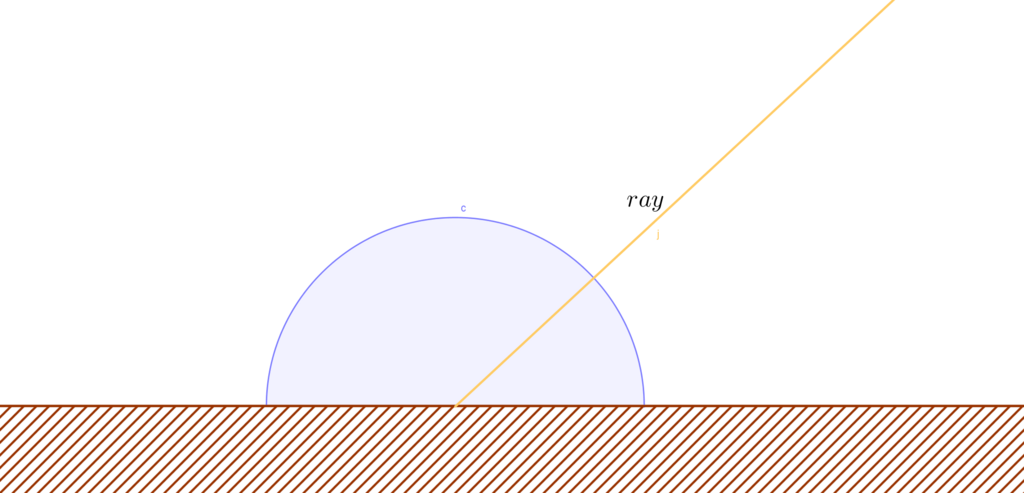
ランバート反射のBRDFを求める

　さて本題です。ここで導出に必要な物理量をしたの表のように定めます。

物理量	記号
放射束	$\Phi$
放射照度	$E$
放射輝度	$L$
反射率	$\rho$
立体角	$\omega$
BRDF	$f_{r}$
面積	$A$

シチュエーションによって、添え字に $i$ (入射)や $r$ (反射)をつけることがあります。

まず、反射率 $\rho$ を定義します。反射率は、

$\displaystyle \rho = \frac{d\Phi_{r}}{d\Phi_{i}}$

と定義されます。入射する光のエネルギーと反射する光のエネルギーの比ということで、イメージはしやすいですね。
さて、この反射率の定義に沿ってBRDFを導出したいのですが、そのためには放射束から放射輝度まで次元を落としていく必要があります。

入射放射束を変形する

まずは入射放射束を変形します。とはいえ放射束の定義に従って

$\displaystyle \begin{align} \Phi_{i} &= \int_{A}\int_{\Omega} \left( \omega' \cdot n \right)L_{i} \left( x, \omega' \right)d\omega'dA \\ &= \int_{A}E(x)dA \\ d\Phi_{i} &= E(x)dA \end{align}$

反射放射束の変形

　次に反射放射束を変形していきます。同じように定義から攻めていくと

$\displaystyle \begin{align} \Phi_{r} &= \int_{A}\int_{\Omega} \left( \omega \cdot n \right)L_{i} \left( x, \omega \right)d\omega'dA \end{align}$

ここで、ランバート反射した放射束は立体角によらずに一定なので

$\displaystyle \begin{align} \Phi_{r} &= \int_{A}L_{r} \left( x, \omega \right)\int_{\Omega} \left( \omega \cdot n \right)d\omega dA \\ d\Phi_{r} &= L_{r} \left( x \right) dA \int_{\Omega} \left( \omega \cdot n \right)d\omega \end{align}$

また、レンダリング方程式を参考にして

$\displaystyle \begin{align} L_{r}(x) = \int_{\Omega} \int_{A} f_{r}(x, \omega, \omega') \left( \omega \cdot n \right) L_{i}(x)dAd\omega \end{align}$

ここでも $f_{r}$ や $L(x)$ は立体角に依存しないので、

$\displaystyle \begin{align} L_{r}(x) &= f_{r,d}(x) \int_{\Omega} E_{i}(x) d\omega \\ &= f_{r,d}(x)E(x) \end{align}$

となるので、

$\displaystyle \begin{align} d\Phi_{r} = f_{r,d}E(x)dA\int_{\Omega}(\omega \cdot n)d\omega \end{align}$

反射率からBRDFを求める

　さて、ここまで来たので簡単なのですが

$\displaystyle \begin{align} \rho &= \frac{d\Phi_{r}}{d\Phi_{i}} \\ &= \frac{f_{r,d}E(x)dA\int_{\Omega}(\omega \cdot n)d\omega}{E(x)dA} \\ &= f_{r,d}\int_{\Omega}(\omega \cdot n)d\omega \end{align}$

ここで $\omega, n$ は正規化されているので、

$\displaystyle \begin{align} \int_{\Omega}\cos \theta d\omega &= \int^{\frac{\pi}{2}}_{0}\int^{2\pi}_{0}cos \theta \sin \theta d\phi d \theta \\ &= \pi \end{align}$

drumath.hatenablog.com

となるので、