2022-12-10

IwakenLabの技術書典13サークル参加を振り返る

はじめに

本記事はIwakenLabアドベントカレンダーの10日目の記事です。

技術書典 13 に参加してきました

2022 年 9 月 10 日～ 9 月 25 日まで開催されていた技術書典 13 に IwakenLab でもサークル参加して本を頒布しました。結構時間がたってしまいましたが、その時の振り返りができたいなかったのでこの機会にと思い筆を執った次第です。

本記事の内容と対象読者

本記事ではタイトル通り、技術書典に参加してきた振り返りをしていきます。具体的には次の時系列に沿って何をしていたのかを振り返りたいと思います。

企画段階
執筆準備
執筆
イベント中～イベント終了

コミュニティの中の複数人が集まって本を書くということについて、どんなモチベーションで始まってどのように運営していったのかを書きたいと思います。もし所属している団体・サークル・コミュニティで技術書典に出てみたいと思っている方には、もしかすると参考になるかもと思いました。

筆者について

筆者は現在、Unity・AR エンジニア（学生）をしています。もともと記事や本を書いたり LT 登壇をしたりするのが好きな性格で、 2022 年 12 月の段階で技術書典には 3 回サークル参加し、4 冊の本を頒布してきました。4 冊の本の内訳は次のようになっています。

ｎ	参加イベント	形態・名義
1 冊目	技術書典 11	合同本（2 人）・身内サークル
2 冊目	技術書典 12	個人サークル
3 冊目	技術書典 13	合同本（4 人）・IwakenLab
4 冊目	技術書典 13	個人サークル

IwakenLab で参加する前にすでに 2 回サークル参加をしていたので本の執筆についてはノウハウがある状態でしたが、対外活動をちゃんと行っているコミュニティで合同本を書くのは初めてでした。

IwakenLab について

IwakenLabとは、イワケンさんが主催する技術好き学生支援コミュニティです。VR/AR をはじめとする様々な技術が好きな学生・社会人が集まり、Discord 上でわいわいしている場です。普段はあまり IwakenLab として何かを行うことは少なく、どちらかというと活動の主体はメンバー個人で、それぞれがやっていることに対しほかのメンバー・メンターと議論することが多いです。技術書典の参加に関しても、IwakenLab としてというより IwakenLab の本という場を活用して個人の成果物を増やしたいよねという目的で行われました。学校のサークルとちょっと違うのはそこかもしれません。

参加メンバー

IwakenLab のメンター・メンバーの 4 人で参加しました。一緒に参加してくれた 3 人にはとても感謝です。

イワケンさん
- IwakenLab 主催・メンター
- Microsoft MVP
- IwakenLab をはじめ 3 つのコミュニティリーダーをされているすごい方
とうとうさん
- IwakenLab メンバー
- VRChat が好きで Unity もサーバーサイドもできちゃうすごいエンジニア人（えんじにあんちゅ）
Kenty さん
- IwakenLab メンバー
- AR に限らず面白そうなことをすぐ試す行動力モンスター。めっちゃ話聞くのがうまい。
にー兄さん（筆者）
- IwakenLab メンバー
- ネコをモフることが得意

筆者の役割

書典 13 の時点で、筆者を除いた 3 人は初サークル参加で Re:VIEW を使った執筆経験もありませんでしたので、筆者は全体のマネジメントをしたり技術サポートをしたりという立ち回りになりました（編集長と呼ばれていました）。具体的には次のようなサポートを行いました。

執筆技術選定
執筆リポジトリの整備
執筆ルールの策定
執筆環境構築のサポート（講習会の開催など）
スケジュール作成
本の編集作業
表紙の作成

サークルアカウント管理はイワケンさんにお願いしました。なのでイワケンさんにはサークル参加手続きや銀行口座の紐づけ、入稿などの作業をしていただきました。アカウントには銀行口座などが必要だったため、コミュニティの代表をしている人にお任せするのが良いと思われたためです。

企画～執筆前

プロジェクト始動前

きっかけは自分が技術書典 12 に参加したときに、イワケンさんが「次は一緒にやりたい」と言ってくださったことでした。ということでとりあえず Discord にチャンネルだけ作り、13 の具体的なスケジュールが出たら動き出すことにしました。

プロジェクト始動

6 月 16 日に公式から書典 13 の開催アナウンスが出ました。これを機にプロジェクトが始動という感じです。この時に確定したスケジュールは以下です。

6/22 ～ 7/24：サークル参加申し込み
9/10 ～ 9/25：技術書典オンラインマーケット
- ここで 9/7 くらいが電子書籍のデッドラインかなぁという見立てになる

まずは 7/24 日の参加申し込み締め切りまでに参加メンバーを募集する動きをしました。興味のある人向けにチャンネルで公式イベントのアナウンスをしたり、キックオフミーティングを行いました。この時点である程度メンバーが参加することがわかったので、サークル参加することが確定しましたがメンバーはもっと後の 7/31 に確定させました。

参加申し込み

7/23（締め切り前日）にサークル参加申し込みをしました。

キックオフミーティング

キックオフミーティングでは、興味がある人向けに以下の内容について伝えました。

技術同人誌とは / 技術書典とは何か
執筆する本の概要
本を書くための知識
GitHub Oriented Writing
- GOW について
- IwakenLab でのルールについて
相談したいこと・やることリスト

キックオフの中である程度開発環境について方針決めも行いました。自分が発表した時には、環境構築が難しい場合には Re:VIEW 環境以外でもマークダウンを使える選択肢を用意していたのですが、せっかくなのでみんな Re:VIEW の環境構築に挑戦しようという話になりました。 Re:VIEW の環境には少し苦労した人もいましたが、最終的にこの決定は良かったと思っています。

ちなみに GitHub Oriented Writing に関しては過去に記事を書いておりますので、詳しくはそちらをご覧ください。

zenn.dev

執筆リポジトリの整備

執筆リポジトリの整備を行いました。キックオフが終わった後で、だいたい執筆ルールの方針も決まっており、扱うツールの選定も済んでいたので、あまり迷わずに行えました。具体的には以下のようなことを行いました。

Re:VIEW 環境を導入したプロジェクトファイルの整備
メンバー執筆用のファイルの用意
issue テンプレートの準備
GitHub Action の整備

スケジュールの共有

リポジトリの整備が済んだ状態で、メンバーには今後のスケジュールを共有しました。この時が 8/10 だったので、締め切り 1 か月前という感じです。これは個人的にですが、同人誌の執筆には 1 か月がちょうどいいと思っています。あまり短いと原稿が終わらないのもありますが、あまり長くするとモチベーションが低下してしまいます。同人誌は本当にモチベーションが大事なので、あまり時間をかけず、気持ちが上向きになっている短期間でなるべく仕上げるようにしたいです。

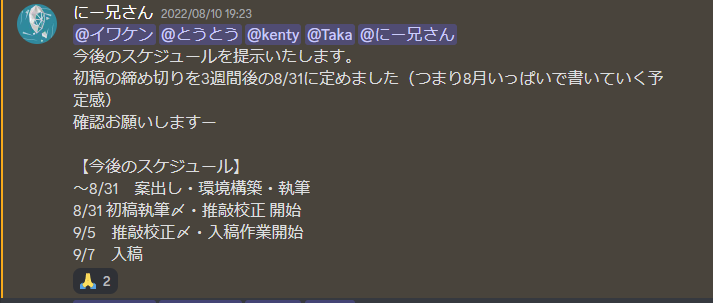
今回は合同本で一人で一冊書くわけではないので少し短めでいいと思ったのと、Re:VIEW を使った執筆に慣れていない人がいるのを考慮して、初稿までを 3 週間弱としました。

環境構築もくもく会

スケジュールを共有したあとは環境構築もくもく会を行いました。 Re:VIEW の環境構築はちょっとめんどくさいので、ここはみんなで足並みをそろえたいよねということで開催しました。ここでは各自の手元で以下の機能が動作するのを確認しました。

vscode で Re:VIEW 拡張機能をインストール
Re:VIEW のプレビューが表示される
textlint で推敲校正ができる
Docker で原稿を PDF 出力できる（一部のメンバーのみ）

環境構築会は本当にやってよかったと思いました。元々は参加する人たちに時間を取ってしまい申し訳ないと思っていたのですが、なんだかんだ細かいポイントで躓いたりツールの理解度も揃えられたりしたので、この時間は必要だったなと思います。

執筆～入稿

粛々と執筆

環境構築の甲斐もあり、そこからはメンバーそろって執筆を行えました。細かい質問などは非同期的に discord に投げてもらい、都度自分が対応しました。質問の例としては以下のものがありました。

vscode の Re:VIEW 拡張では画像がプレビューされない
- これは今のところ我慢するしかなさそう......
数式がプレビューされない＋ vscode 上でエラーになってしまう
- これも我慢するしかなさそう......エラーになるのは本当に不便
- 一回拡張機能のコードを見て見たのですが、当時はちょっとめんどくさそうに感じた記憶があります
コードがはみ出てしまう時はどうすればよいか
- 今回はなんとかコードに改行を入れながら進めました
- サンプルコードのレビューを行い、コード量を短くしたこともあった

初稿締め切り

初稿の締め切り、つまり 8 月末日の 1 週間前に進捗確認のアナウンスを出しました。正直この時点では自分もメンバーもそこまで完成していなかった気がします。そして結局締め切りの日に一番進捗を出しました（よくない）

レビュー

原稿を書いた後はみんなでレビューをすることになっていました。

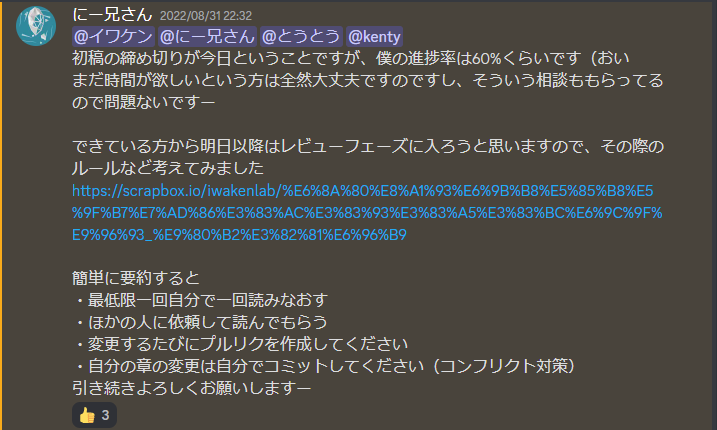
筆者も普通に締め切り過ぎていましたし、まぁこの日に終わらなくても大丈夫だろうと思っていたので終わってない人も継続で書いてもらっていました。画像にもありますが、レビューについてルールも決めました。

最低限一回自分で一回読みなおす
ほかの人に依頼して読んでもらう
変更するたびにプルリクを作成してください
自分の章の変更は自分でコミットしてください（コンフリクト対策）

最終的に、メンバー全員が他のメンバーの記事に一回は目を通し、誤字脱字やよりよい記法などをレビューしあいました。ここには書いていないですが、レビューして気になった点を issue で出すという動きが自然と生まれていて、後半はその形式でやっていました。

表紙

表紙作成は反省点が多いです......。というのも最後の最後まで表紙についてあまり議論できておらず、締め切りギリギリまでずっとやっていたタスクだったからです。最悪自分が巻き取ればいいかと思っていたのですがやはり最終的にそうなりまして、ちょっと苦戦しつつなんとか背景グラフィクスを Unity で作成し、文字組をイラレでやって表紙データを作成しました。

結局最終版の画像が上がったのが締め切り日の AM3:22 だったので、深夜まで粘っていました。ここは本当に、メンバー(特にイワケンさん)にギリギリまで心配をかけてしまったので反省です......。

入稿

表紙データが上がった後、イワケンさんが 4 時半くらいに入稿データの審査に出してくれました（圧倒的感謝）。そこからは目立った事故もなく審査が通り、自動的にマーケット開催時に購入可能になりました。

イベント会期中～終了

イベント会期中は特に大きな仕事はなく、ちょくちょく宣伝を挟みつつ売り上げ状況の確認などをしていました。

おわりに

ひととおり書典 13 での執筆活動について振り返りました。 4 人という規模で合同本を作ったのは今回が初めてだったため、上手くいかないこともありメンバーには心配させてしまったこともありましたが、無事本を出せてよかったです。また、IwakenLab としても書典参加は初めての試みであったため足場づくりの部分が多かったですが、そのおかげで次回以降参加することになったとしたらノウハウをそのまま使うことができるのではないかと思っています。協力してくださったメンバーには圧倒的感謝です。

また、もしこの記事がこれからコミュニティで技術同人誌を書いてみたい人の助けになれば幸いです。最後まで読んでいただきありがとうございました。

2020-12-02

Fusion360にBlenderで作ったモデルをインポートする

この記事は愚者っとCorp.アドベントカレンダー2020の2日目の記事です。

はじめに

どうも、にー兄さんです。自分は長らくBlenderを使っているのですが、Blenderで作ったモデルをFusion360で使いたいと思ったので色々試したところ直接的な記事はなかったので小ネタとして書きたいと思います。

はじめに
- 対象読者
Fusion360にBlenderで作ったモデルをインポート
おわりに
- 参考

対象読者

Fusion360をインストールしている
Blenderを使ったことがある

レベル感は、自分が素人なので入門者向けとなります。

Fusion360にBlenderで作ったモデルをインポート

Fusion360でインポートするには

Fusion360は.stlファイルと.objファイルを外部からインポートすることができます。方法としてはメニュー＞挿入＞メッシュを挿入コマンドによってインポートできます。 f:id:drumath:20201202164422p:plain ということでまずはBlenderから.objファイルをエクスポートする必要があります。

BlenderでOBJファイルを出力する

まずはBlenderで適当なモデルを作るor持ってきましょう。試しにこちらのスタンフォードバニーを使ってみます。 f:id:drumath:20201202163933p:plain 位置がずれていたので調整したり、ポリゴン数を削除してみたりしました。 f:id:drumath:20201202164248p:plain

そのあとにエクスポート＞wavefront(obj)を選択し、適当な場所に出力します。

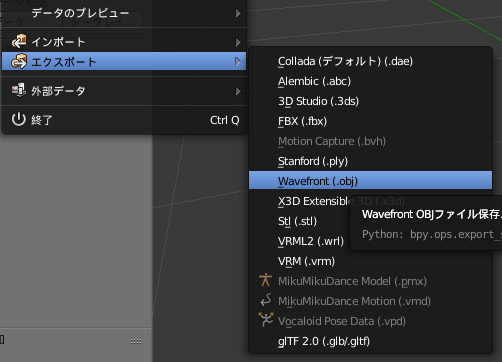
f:id:drumath:20201202164313p:plain

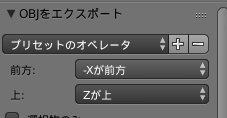
この時に、Fusion360はZアップの座標系を採用しているので、こちらでもZを上にしておくといいでしょう。

f:id:drumath:20201202164623p:plain

Fusionでメッシュデータを使えるようにする

Blenderで出力したOBJファイルを冒頭で説明したメッシュの挿入コマンドでインポートします。そうすると、Fusionにメッシュが生成されます。

f:id:drumath:20201202164653p:plain

しかしこのままでは編集することができないので、このメッシュデータをソリッドデータ(Brep)に変換する必要があります。

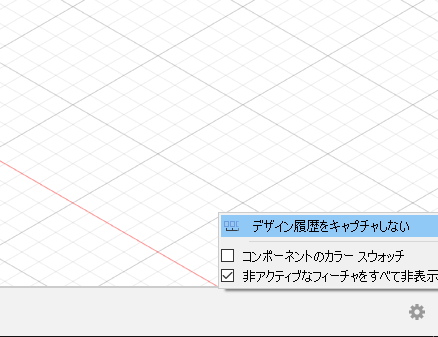
まずは右下の歯車ボタンを押して「デザイン履歴をキャプチャしない」を選択します。

f:id:drumath:20201202170524p:plain

そのあとにメッシュを右クリックすると「メッシュからBRep」というメニューがあるのでクリックします。

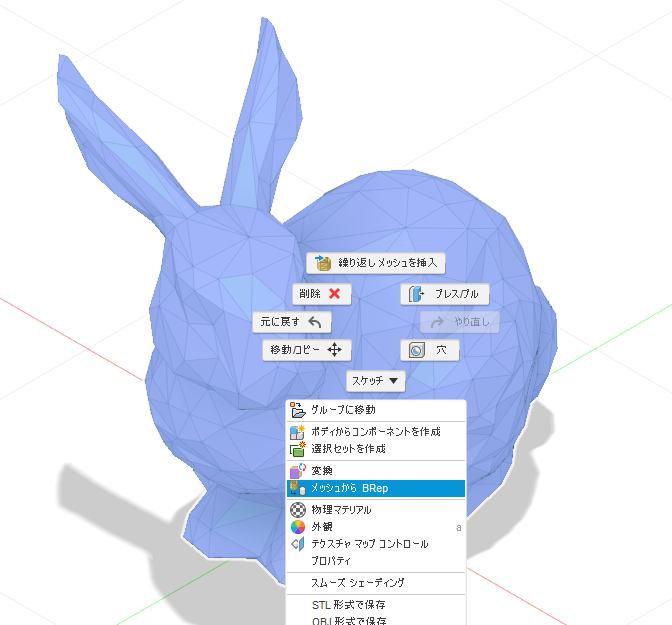
f:id:drumath:20201202170623p:plain

すると、無事にメッシュがソリッドデータになり、Fusionで編集できる形になりました！

f:id:drumath:20201202170742p:plain

おわりに

今回はすごい小ネタとして記事を書きました。何かの参考になれば幸いです。

次の担当は、また私で「VFX GraphをTimelineで制御する」という内容になると思います。

参考

2020-12-01

夏から秋にかけて本を読了したので振り返ってみる

この記事は愚者っとCorp.アドベントカレンダーの 1 日目の記事です。

はじめに

今年もアドカレの季節がやってきましたね......。去年は Qiita に技術記事を 2 本ほど投稿したのですが、今年は技術記事以外もやっていこうと思います。というのも、ひっそり活動してたごった煮同人サークルでアドカレやってみるか!!ってなったからです。

でもアドカレってムズカシデス......。普段なら「ネタがあったから記事を書く」わけですが、「記事を書くためにネタを探す」必要がありますからね。最近何やってたかなぁ？　と思いを巡らせたところ、読書をしていました。普通すぎないかと思うかもしれませんが、なんだかんだ読書というものをちゃんとやってこなかった自分にとっては少し特別なことだったので、この機会に一筆したためたい思いました。

はじめに
読んだ本を振り返る
本を読むことについて考える
- ネット記事と本
- 物理本との付き合い方
おわりに

読んだ本を振り返る

ところで、みなさんは「本」と聞いて何を思い浮かべるでしょうか？自分の場合は趣味の影響もあって、技術書や理系書などの専門書が最初に思い浮かびます。そういえば小説ってあまり読んだことないんですよね、ちゃんと読んだのは小学生の頃に読んだトム=ソーヤーの冒険くらいなんじゃないかな......。

まぁそんなことはさておき、今回テーマにしている「本」とは技術書(とそれに近い本)の事を指しています。期間は 8 月の中旬から 11 月の中旬までの約 4 か月くらいで、4 冊の本を読みました。

いちばんよくわかるWebデザインの基本きちんと入門

いちばんよくわかるWebデザインの基本きちんと入門　レイアウト／配色／写真／タイポグラフィ／最新テクニック

作者:伊藤庄平,益子貴寛,久保知己,宮田優希,伊藤由暁
発売日: 2017/02/25
メディア: Kindle版

初めて読んだデザインに関する本だったのですがデザイン素人の自分でもわかりやすく読めました。Web がテーマになっている本ではありますが、デザインの基礎から説明してくれるので他のメディア、プラットフォームでも使えそうな知見が詰まっています。

レイアウト、配色、タイポグラフィなどの、デザインをするにあたって必要な要素ごとにセクションが分かれていて、それぞれビジュアルを交えて丁寧に説明されています。加えて各セクションの最後に実例デザインという項目があり、実際に使われている参考になりそうなサイトの一覧が載っています。

個人的には配色のセクションが結構好きで、色を構成する要素であったり色の組み合わせだったりをたくさん図を使って説明されているので読んでいて楽しいです。他にも HTML/CSS の具体的な tips が載っていたり最後にはマーケティグに関するセクションもあるので、実践的に使える知見が得られます。

自分はデザインをほぼ勘に頼ってやってきた人間なので、グラフィック系の制作物は行き当たりばったりで作っていました。しかしデザインにもちゃんと理論があることを理解することで、これまで作ってきたものを批評できるようになり、また身の回りにあるデザインに対してもその意図を汲み取りやすくなったのではないかと思います。

ユニティちゃんトゥーンシェーダー2.0　スーパー使いこなし術

実践! ユニティちゃんトゥーンシェーダー2.0 スーパー使いこなし術

作者:ntny,浦上真輝,前島,あいんつ,ぽんでろ,小林信行
発売日: 2019/09/27
メディア: 単行本

某 LT イベントで、嬉しいことに賞品としていただきました(？) 以前からトゥーンシェーダにすごい興味があって勉強したいと思っていたので読み始めました。

そもそもこの本が何についての本なのか説明したほうがいいかもですね。(わかってる人は読み飛ばしていただいて結構です)

シェーダとは、ざっくり言うと 3D モデルの見た目を定義するプログラムの一種で、これを使うことで3D ゲームや 3D アニメーションの中でモデルやシーンの見た目を変更することができます。その中でもトゥーンシェーダというのは、字のごとく漫画やアニメのような見た目を表現するためのシェーダを指します。そして、Unityで使えるトゥーンシェーダの代表的なものとして「ユニティちゃんトゥーンシェーダー」というものがあり、この本はユニティちゃんトゥーンシェーダーについてがっつり書かれた本なのです。普通に商業誌なのがすごい。以下、ユニティちゃんトゥーンシェーダーをUTSと表記します。

UTSはとても汎用的なトゥーンシェーダなので色々な設定項目があり、実際に使おうとすると「どうすればいいんだ......」となりがちです。そこでこの本ではUTSで用意されている機能やプロパティを網羅的に説明しています。構成は以下の通りです。

コンセプト編
入門編
応用編
作例編
リファレンス編
UTS2作品ギャラリー

コンセプト編や入門編では、UTSが何を目指して作られ、どのようなことができるのかなどの概要を知ることができます。トゥーンシェーダの基本的な機能から、具体的な作例も紹介されており図を見ているだけでも多くの知見が得られます。UTSは使いきれないくらい本当に多くの機能があるので、このセクションを見ることで「１つのマテリアルでここまでできるのか......」と感動しました。

応用編と作例編はとにかく情報量がすごいです。「キャラクターを作る」というプロセスはシェーディングだけでは完結しせず、キャラクターのモデルを作ってリギングしてモーフを作ってUnityで読み込んでマテリアルを設定して......と様々なステップがありますが、応用編ではその前段階であるキャラクターの仕様策定の段階からのプラクティスを説明しています。このセクションを読むことでキャラクターを作る一連の流れを知ることができます。プロの人たちがどんなことに気を使ってキャラクターを作っているのかという情報がそのまま載っているので、すごい貴重な文献だと思います。作例編では3人のクリエイターの方が異なるテーマに沿ってキャラクターを作っていく様子が説明されています。UTSを実践的に使うときにどのようなプロパティを使うのか、各種素材をどう作るのか、そんなツールを使うのか、などの情報が載っています。

リファレンス編では、その名の通りUTSで使える各種シェーダ、それぞれのプロパティを網羅的に説明されています。モノホンのリファレンスです......。

いや、何度も言うけどこれ本当に商業誌だよな......？ここまでニッチで高濃い内容の本って本当に貴重だと思うので、UTSだけではなくトゥーンシェーダに興味がある人は読んで是非読んで欲しいです。本当に情報量がすごい。

誰でも作れるUIデザイン入門

誰でもつくれる！UIデザイン入門　～機能するUIの基本と実践～

作者:ななうみ
発売日: 2020/07/30
メディア: 単行本（ソフトカバー）

2冊目のデザイン関連の本です。友人がUIデザインをしたいと言っていた事がきっかけで自分も興味をもったので本屋さんで買いました、気分で。本を気分で買うパターン多いな、まぁそれくらいの思い切りじゃないと3000円が相場の専門書って学生はあまり買えないですよね。

この本の構成は以下の通りです。

基本のキ編
IA・レイアウト編
オブジェクト・造形編
フォント・カラー編
レイヤー・アニメーション編
これからの学び編

この本の特徴は、なんといってもかわいいキャラクターの挿絵があちこちにあるところだと思います。そのおかげでとてもポップな雰囲気で読みやすいです。設定として、UIデザインを勉強したい女の子がUIデザインを研究している博士（？）に教えてもらうというストーリーになっています。

この本もタイトルにある通り入門本になります。よってデザインの基礎的な部分の説明が多く、特に2,3,4章はWebデザインの本で読んだ内容の復習になってよかったです。逆にプラットフォームを限定しない分、より抽象度の上がった内容になった気がしました。各セクションで共通して、「機能面」と「心理面」の両方でより良いものをデザインとして採用するとよい、ということを繰り返し訴えられていて、UIというのが「システムと人間をつなぐもの」ということをちゃんと再認識できました。

SLAM入門

SLAM入門: ロボットの自己位置推定と地図構築の技術

作者:友納正裕
発売日: 2018/03/03
メディア: 単行本（ソフトカバー）

前述した3つの本とはちょっと毛色が違い、理系専門書という感じのチョイスになります。こちらもまず「SLAMってなんぞや」から話さないといけないですね。 SLAMとはSimultaneous Localization and Mappingの略で日本語に訳すと「自己位置推定と環境地図構築の同時実行」という風になります。これだけだとちんぷんかんぷんですが、例えば車の自動運転の実装といったシナリオではコンピュータが自律して目的地まで車を走らせる必要がありますが、その時に「車が現在どこを走っているのか(どこを走ってきたのか)」や「周りの環境がどうなっているのか」の情報が必要です。これを実現するためにSLAMが必要になります。自動運転だとちょっと実感がわきにくいですが、自律して部屋の掃除をしてくれるロボットであるルンバなどは、まさに部屋においてSLAMを実行しています。 SLAMはこのように、ロボットが自立して走行するシチュエーションに対して有効なメソッドになります。本の構成は以下の通りです。

はじめに
SLAMの基礎
SLAMの入出力
SLAMシステムの具体化
本書のプログラム
オドメトリによる地図構築
スキャンマッチング
スキャンマッチングの改良
センサ融合による退化への対処
ループとじ込み
SLAMの数学的基礎

目次を見るとわかるのですが、一番最後に付録としてSLAMで登場する数学がまとめてあります。自分は本編を読む前に、まず11章から読んでナンモワカランって言いながら線形代数や確率統計の復習をしました。本編で結構11章が参照されるので、先に読んでおいてよかったと思います。

この本の特徴は、SLAMが実装されているプログラムがほぼそのまま載っているということです。もちろん理論の説明はしっかりしているのですが、6章以降では理論の説明の後に実装されたプログラムとその実行結果が載っているので説得力は高いです。ただ、個人的にプログラムはシンタックスハイライトと宣言/Usageへジャンプ機能がないと読めないので、さらっと流しました。この本のレベル感として、自分のような理系大学生にはちょうどいいのではないかと思います。線形代数や連続確率の微積が絡むので高校生にはちょっときつい内容だと思います。それでもってSLAMのホントに初歩から教えてくれるのでプログラムをある程度書いたことがあるけどSLAMを実装したことはないくらいの層には結構ありがたいです。逆にSLAMの初歩的な手法を使うため、この本の内容をそのまま使ってしまうと実践ではパフォーマンスが不十分である可能性があると思われます。

そもそも自分はあまりロボット制御には詳しくなく、趣味やアルバイトで点群を扱った開発を経てSLAMに興味を持ったのですが問題なく読めました。おそらくこの先建築分野やロボティクスで点群を用いたセンサリングは普通に使われていくと思うので、教養として学べてよかったです。

本を読むことについて考える

この数か月、自分は読了にこだわってきましたが、ここで少し思ったことがるので書いてみようと思います。とはいえ自分は図書館学などに精通しているわけではないので、ほんの「お気持ち」になります。あくまで個人の意見としてとらえていただけると幸いです。

ネット記事と本

現代ではインターネットや検索エンジン、SNS、ブログサービスなどによって「たいていの欲しい情報は検索すれば手に入る」ようになりました。それはプログラムを書いているときでも授業の課題をしているときでも、音楽や動画を視聴したい時でも、ネットニュースを見る時でも共通です。実際自分もわからないことがあったらまずググりますし、逆にググれば出てくる情報は興味がなければ努力して覚えようとはしません。このような状況で本に価値ってあるのでしょうか？特定方面から刺されそうな問題提起なので早めに自分の意見を述べると、あると思います。ここでいったん本とネットの情報を比べてみましょう。

	ネット情報	本
検索の手軽さ	手軽	ある程度の根気が必要
公開の手軽さ	手軽	手間・お金・知識量が必要
値段	一部で有料だが無料の場合が多い	基本的に有料
情報の信頼性	イマイチ	基本的に信頼できる
検索結果の総数	分野によるが公開の手軽さゆえに膨大になることも	分野によるが入門に偏る場合がある
情報の鮮度	比較的新鮮	古いこともしばしば
物理的な占有度	ほぼなし(ストレージデバイスを考慮しなければ)	情報量に比例して大きくなる(物理本に限る)
得られる知識の形態	(多くの場合)断片的	体形的

パッと考えられる項目を適当に列挙したのですが、本に不利になるような物が多くなった気がしますね。そして全体的に見てネット記事のほうが手軽という印象です。しかし反対に、本における重要なメリットが示されています。それは体形的な知識が得られる点です。ネットで検索すればすぐ情報が手に入る時代だからこそ、このメリットは重要なのだと考えます。

自分は以前、本当に自分の望む事以上の情報が付随してくる本という媒体に対して「コスパが悪い」と感じていました。本は好きでしたが、買った本は全部読み切るなんてことはせず、気に入った場所だけ読んで終わりにしていました。ゆえに専門書よりも雑誌の方が好んでいた時期もあった気がします。それ自体は別に悪いことだとは思っていないのですが、せっかく本が手元にあるのに断片的な情報しか取得できないというのは勿体ないのではないかと、今では思います。(学校の授業でも「こんなの調べれば出てくるじゃん」思いながら受けてることもありますが、こちらも同様ですね)

今回本を最後まで読むということをしてみて、(改めて)学習の本質は、体形的知識による概念の抽象理解なのではないかと感じました。目先の問題にだけ対処すればよいのであれば、ネットで探した小手先の技術だけでどうにかできます。しかし生きていくうえでそんなことばかりではないと思います。特にこれから社会人なって専門的な知識が必要になってくると、おそらく「よくわからん何か」に遭遇することでしょう。でもネットにはその「よくわからん何か」に対して「よくわからん事」をすれば「よくわからんけど解決する」という情報が落ちている可能性があります。いやもうそんなことス〇ックオー〇ーフローを漁ればよくわからん英語(ときどきよくわからん日本語訳)でいくらでも出てくるんです。そうなってくると小手先の知識で対処するには限界が来る気がします。しかし、分野に対してある程度の体形的知識があれば「よくわからん事」を提示されたときに、だいたいの意図がつかめます。また、他分野であっても近い領域に体系的な知識があれば、それと比較しながら学習することで理解が早く深くなると思います。知識が多いことに越したことはないのですが、その知識がどのように頭の中にあるのかは概念理解においては重要だと考えます。それゆえに、体形的知識が得られる本という媒体は、学習においてとても価値があると考えます。

物理本との付き合い方

話しが変わりますが、私はいわゆる物理本が好きで、本を買うときはだいたい本屋さんだったりネットで買う時も電子書籍ではなく物理本で買います。今述べたように、物理本と比較されることが多いのは電子書籍ですよね。本当に電子書籍って便利だと思っていて、ネットで買えるから店頭まで行かなくていいし、本棚の場所をとらないし、デバイスさえ持っていればいつでも開けて、ページ数が多い本でも重さは0です。

それでも自分は物理本が好きです。前から漠然と物理本を好んでいたのですが、最近になってようやくその理由を見つけられた気がしますので、せっかくの機会なのでちょっと書きたいと思います。とはいえ、電子書籍と比べることはしたくないです。電子書籍の便利さはすでに自覚していますし、不特定多数に向てた意見するにはあまりにも電子書籍のメリットが多すぎて説得力に欠けますし、もはや趣味として別ジャンルなのではないかとすら思うからです。ということで物理本のメリットではなく、物理本をどのように楽しんでいるのかという話になります。

自分は大学関係の何かをしているとき、基本的にパソコンに向かって作業をしています。アルバイト業務もパソコンを使いますし、趣味でもパソコンに向かっています。パソコンで作業をすると、様々なタスクが瞬時に切り替えられたり並行して進められたりしてとても作業効率が上がります。(ダウト。Twitterを常時第3ディスプレイに表示しているのでそんなことはない）スマホも同様で、Youtubeで動画を見ているときにSlackやDiscordでメッセージを受信したらすぐ切り替えて返信できます。名前のごとくスマートに物事を進められます。ただ、自分の場合はずっとこの状態を続けていると精神的に疲れてしまうようで、効率やコストパフォーマンスと逆行した趣味に逃げることはしばしばです。最近はコーヒーのハンドドリップとかしてます、マシンを使えば手間いらずで飲めるコーヒーをわざわざ15分くらいかけて淹れてます。コーヒー豆はお湯を注ぐと状態変化が激しくなるので、常に豆の状態を見ながらコーヒーを抽出する必要があり、この15分間は基本的にコーヒーの事しか考えてません。でもほんの15分でも、目の前の事だけに集中することができるこの時間がとても愛おしく感じます。

読書の時間も同じで、パソコンやスマホから膨大に流れてくる情報から一瞬目を背けて、目の前の物事に集中でいる趣味としてとらえています。それこそコーヒーを淹れて本を読む時間は至高です。毎秒やりたいところですが、なかなか本を読む時間ってとれないものです。自分は8，9月にWebデザインの本とUTSの本を読了しましたが、その期間は平日ずっとインターンでフルタイムの業務をしていました。そのなかで本を読むとなると結構きつかったのですが、業務が始まる1時間前に朝の読書の時間を作ったり、夜眠る前の1時間を読書に使うなどしていました。たぶん今やれって言われたらできないかもですが、あのときはそれほどにモチベがありました。そのモチベの発端も、ずっとパソコンに向かって1日が終わるのがちょっと辛かったからではないかと今は思います。

そんなことで自分は、ある種の現実逃避のような付き合い方を物理本としてきました。冒頭で電子書籍と比較しないといった手前申し訳ないのですが、電子書籍だと多分こうはいかなかったのではないかと思います。いや、電子書籍専用のデバイスを使えば解決でいるのかもしれませんが、おそらく電子機械から離れることによってスイッチが切り替わっていた可能性も無きにしも非ずなので、そこは微妙ですね。ちょっと最後にしてはオチがつかなくて申し訳ないのですが、本との付き合い方の一つとして、参考になったのでしたら幸いです。

おわりに

読書に関して記事を書くとは思っていなかったのですが、実際書いてみると結構楽しかったです。アドカレ1日目ということで軽い内容にしようと思っていたのですが、調子が乗ってきたのか分量多めになりましたね......。まぁでも漠然と頭の中で思っていたことを文章で整理できたので、いい機会になったと思います。

次の愚者っとCorp.アドベントカレンダーは、担当はまた自分で「LTのすゝめ」という内容になると思います。

2019-01-06

身内卓で構築したクトゥルフ神話TRPGインフラ

クトゥルフ TRPG

どうも、にー兄さんです。
新年あけましておめでとうございます。
2019年もどうぞ、本ブログをよろしくお願い致します！

ということで新年一発目の記事はクトゥルフ神話TRPGについて書きます。
技術記事...とは違うかもしれませんが、最後までお付き合いいただけると嬉しいです！

【目次】

TRPGってなんだ？
オンセって何かと面倒くさい
- どどんとふ入ります？ーいや、面倒だしいいよ
- そんな装備で大丈夫か？大丈夫だ、問題ない。
TRPGインフラ？
我が卓のインフラ
最後に

TRPGってなんだ？

TRPGをご存じない方もいらっしゃると思うので簡単に紹介します。
TRPGとは、テーブルトーク・ロールプレイングゲームの略語で、複数人で対話(ロール)によってプレイヤーキャラクターの行動を決定しながらゲームクリアを目指すテーブルゲームです。言葉では少しわかりずらいと思うので、実際にプレイしている動画(リプレイ動画)をご覧にあるといいかもしれません。まにむさんの動画がわかりやすくていいので、リンクを貼っておきます。
www.youtube.com

オンセって何かと面倒くさい

TRPGは複数人で集まるため必要があるため、チャットアプリを用いたオンライン・セッション(オンセ)でやることが多いです。
反対に、リアルで集まって顔を見ながらセッションをする方式をオフライン・セッション(オフセ)と言います。

オンセはプレイヤー(以下PL)が離れていてもできるので便利なのですが、機械を使用する点やPLの意思が直接届きづらいことから、
結構めんどくさいし、セッション時間もオフセよりも長くなる傾向があります。

そんなこともあり、TRPGをする際に、ゲーム鯖を用いてやることもしばしばあります。一番有名な鯖はどどんとふ公式鯖ですね。
チャット、ダイスロール、マップ表示、PCコマ表示をリアルタイムで複数人に反映させてくれます。非常に強力なTRPGツールの一つと言えるでしょう。

どどんとふ入ります？ーいや、面倒だしいいよ

ただ、うちの卓では最近どどんとふは使いませんね。
単純にめんどくさいからです。なんと怠惰な..。これほど強力なツールなのに...

使わない理由は明確で、どどんとふがなくても回せるセッションは多いからです。
実際いつもマップ表示したりPCを動かしたりしませんからね。軽めのシナリオだったらいりません。

そんな装備で大丈夫か？大丈夫だ、問題ない。

TRPGはゲーム機を使用しない、軽量なゲームです。
シナリオとキャラシとダイスさえあれば最低限回せます。
オンセで回すシナリオなんてせいぜい２、3時間、多くて4時間くらいが関の山です。

だから普段やるようなシナリオだとどどんとふのすべての機能はいりません。

TRPGインフラ？

TRPGインフラという言葉が必ずしもあっているのかはわかりませんが、「インフラ：下部構造、仕組みを支える物」という意味で私はこう呼んでいます。
ようは、TRPGをするためにどんなツールを使っているのかです。

我が卓のインフラ

さて、私の卓のインフラを紹介したいと思います。
メンバーは8人、セッションで集まる時はだいたい2~4人くらいで回します。

チャットアプリ

チャットはDiscordを使用しています。
実は前まではSkypeを使っていました。SkypeからDiscordに乗り換えた理由は以下の通りです。

軽量
Slackライクに部屋が作れる
botが簡単に作れる
絵文字がカスタマイズできる
デザインが素敵
ゲーム特化

この中にはSkypeに実装してある機能が含まれていますが、いずれもDiscordのほうが性能は上だと判断しました。
一つ目にあげた「軽量」についてですが、前に使っていたSkypeが何か月か前に大型アップデートをしまして、デザイン・操作性ともに一新されてから意識しました。
スマホで開くときにも毎回長いローディング時間...イライラしますよねぇ...。その点軽量なチャットアプリであるDiscordは勝っていました。
部屋が作れるのも結構重宝しています。現在うちの卓で作られている部屋は

一般カテゴリ内
- #General
- #Random
- #ミュート推奨雑談部屋
- #セッション募集部屋
- #おすすめリプレイ紹介
- #共有ドライブ変更報告
- #ジュークボックス
セッションカテゴリ内
- #各種セッション部屋
- #キャラシ提出倉庫
- #セッション部屋(ボイス)
イラストカテゴリ内
- #イラスト倉庫
- #絵チャ場
- #イラスト依頼
開発カテゴリ内
- #Bot実験室

という感じです。部屋は作っておけばログが残るので便利ですし、ピン止めもできます。
discordapp.com

キャラシ

キャラシは自作のExcelテンプレートを作りました。まだ配布は考えてないので詳しくは書けませんが

能力値を入力すると自動でその他のステータスが算出され、
技能値を入力すれば初期値と合算された合計値を吐き出し
それらのデータをグラフを使うことで可視化でき、
さらにA4印刷でちょうどよい大きさに最適化されています。

Excelのいいところは、データの計算と可視化が簡単にできる事ですね。
夏休みに6時間かけて作りました（）

録音

自作です。うちの卓には開発課なる部署が存在し、2名が配属されていますが。
片方のつよつよプログラマがステレオ音源の録音・出力に対応した録音ソフトを作りました。
とても軽量で重宝しています。ありがたや...
配布とか予定あるのかな･･･？

ダイスロール

自作Botです。
↑のDiscordのメリットでBotが簡単に作れるとありましたが、まさにダイスロールbotを作りました。

とはいえ、実際作らなくてもBotは各所に落ちています。そんな中私が作ったbotが目指したのは使いやすさです。

機能をダイスロールだけにしぼり、「\r 1d100<70」みたいなコマンドライクではなく
なんでもかんでも「(数値)(Dかd)(数値)」という書式であれば反応するようにしました。
理由は、チャット中に半角とか普通じゃ使わない文字を打つのがめんどくさいと思ったからです。
pythonの強い文字列処理を使えば普段チャットをするのと変わらない操作感でダイスロールができます。そこはこだわりました。

BGM

Botを入れました。Discordのbotで、rhythmというBotがあります。
シリアスだったらYoutubeから暗いBGMを見つけてくるだけでボイスチャンネルで再生できます。
すばらしいBotです。ぜひ導入してみてください。

tech.kunimaly.com

共有サービス

Googleドライブを利用して、キャラシやセッション録音音声、セッションログを更新します。
これにかんしては導入中なのでこれからの展望というべきかもしれません。
GoogleドライブからGoogle スプレッドシートを利用すれば、オンラインでリアルタイム複数人編集が可能です。
最新のドキュメントがどこでもDL不要で利用できるので、「キャラシがない！」「ログ見たいから送って欲しい」なんてことはなくなります。

絵文字

Discordでは絵文字も自作できます。身内ネタで盛り上がるのも良し、セッション募集チャンネルで参加表明するのも良し。
素晴らしい機能です。

最後に

最初はツールを導入すると結構戸惑うのですが、セッションを重ねるごとに慣れていき、今では普通に使いこなしています。
皆さんも、TRPGインフラを構築し、円滑快適なクトゥルフ・ライフを満喫してみてはいかがですか？
この記事が少しでも参考になれば幸いでございます。

最後までお付き合いいただきありがとうございました。
いあ！いあ！クトゥルフ！

2018-11-23

λ式と再帰を使って連分数を計算するRubyワンライナーでπを近似する

Ruby 数学小ネタ

お久しぶりです。もう定番ネタと化しているπの近似値ですが(諦)、今回は第3弾となります。

πの近似値を連分数で求める

公式

今回参考にした公式が、Wikipediaに載ってます。
wikipedia:連分数#様々な数の連分数展開

引用させていただくと、

$\displaystyle \frac{4}{\pi} = 1+ \displaystyle \frac{1^2}{3+ \displaystyle \frac{2^2}{5+ \displaystyle \frac{3^2}{7+ \displaystyle \frac{4^2}{9+ \displaystyle \frac{5^2}{11+ \displaystyle \frac{6^2}{\ddots } } } } } }$

あ、ちなみに↑の連分数なのですが、はてな記法で書くにはコツがありまして、
私はこんな感じで書いています。

<div style="text-align: center;">
[tex:
\displaystyle \frac{4}{\pi} = 1+
\displaystyle \frac{1^2}{3+
\displaystyle \frac{2^2}{5+
\displaystyle \frac{3^2}{7+
\displaystyle \frac{4^2}{9+
\displaystyle \frac{5^2}{11+
\displaystyle \frac{6^2}{\ddots
}
}
}
}
}
}
]
</div>

余談でした。

さて、問題は連分数をどうやって実装するのかですね

再帰を使う

やはり最初に思い浮かんだのは再帰でした。
イメージとしては

$\displaystyle a_n = n_1 + \frac{n_2}{a_{n-1}}$

これがテンプレートになって、これをイテレートしていくと

$\begin{align} \displaystyle a_n &= n_1 + \frac{n_2}{a_{n-1}} \\ \\ \displaystyle &= n_1 + \frac{n_2}{n_3 + \displaystyle \frac{n_4}{a_{n-2}}} \\ \\ \displaystyle &= n_1 + \frac{n_2}{n_3 + \displaystyle \frac{n_4}{n_5 + \displaystyle \frac{n_6}{a_{n-3} } } } \end{align}$

という具合に求まっていきます。再帰的ですね。

さて問題の上のπの公式をRubyに落とし込むと、こんな感じに

def pi_continued_fraction(num1, num2, loopcount)
  return 1 if loopcount <= 0

  num1 + (num2**2 / pi_continued_fraction(num1 + 2, num2 + 1, loopcount - 1))
end

puts 4 / pi_continued_fraction(1.0, 1.0, 25)

三項演算子の呪い

私「ｎ？このコードもう少し短くできるよね？」

可読性「えっ？(困惑)」

私「三項演算子をすこれよ」

def pi_continued_fraction(num1, num2, loopcount)
  loopcount <= 0 ? 1 : num1 + (num2**2 / pi_continued_fraction(num1 + 2, num2 + 1, loopcount - 1))
end

puts 4 / pi_continued_fraction(1.0, 1.0, 25)

λ式の呪い

私「関数定義はやっぱ一行だよね」

可読性「やめとｋ」

ラムダ騎士団「いいぞ(食い気味)」

私「ラムダ式すこ」

pi_continued_fraction = ->(num1, num2, loopcount) { loopcount <= 0 ? 1 : num1 + (num2**2 / pi_continued_fraction.call(num1 + 2, num2 + 1, loopcount - 1)) }
puts 4 / pi_continued_fraction.call(1.0, 1.0, 25)

ワンライナーの呪い

私「2行...」

可読性「日本では古来から、奇数は縁起が良いと言われてきたらしい」

私「あぁ、三重塔とか五稜郭とか三十一文字とかそうだね」

「「一行にするか」」

puts 4/(pi_continued_fraction = ->(num1, num2, loopcount) { loopcount <= 0 ? 1 : num1 + (num2**2 / pi_continued_fraction.call(num1 + 2, num2 + 1, loopcount - 1)) }).call(1.0,1.0,25)

できればπの近似値をはじき出す関数

pi()

の定義がしたいので、
最終的には

puts pi = -> { 4 / (pi_continued_fraction = ->(num1, num2, loopcount) { loopcount <= 0 ? 1 : num1 + (num2**2 / pi_continued_fraction.call(num1 + 2, num2 + 1, loopcount - 1)) }).call(1.0, 1.0, 25) }.call

となりました。
ターミナルには

> 3.141592653589793

と表示されました。だいたい25項目よりも前には小数点以下15桁は求まるみたいです。

最後に

最後まで読んでいただき、ありがとうございました。

誰か可読性ちゃんを擬人化してくれると嬉しいです。

2018-07-05

レンダラー開発のための測光学覚書　補講　コサインの半球積分

レン覚数学

補講

前回書いた記事に、

$\displaystyle \begin{align} \int_{\Omega} \cos \theta d\omega &= \pi \end{align}$

という式が出てきましたので、この解説を補講という形で解説したいと思います。

まず、Vol.1の記事から以下のことがわかります。

$\displaystyle \begin{align} d\omega = \sin \theta d \phi d \theta \end{align}$

drumath.hatenablog.com

このことから、

$\displaystyle \begin{align} \int_{\Omega} \cos \theta d \omega &= \int^{\frac{\pi}{2}}_{0} \int^{2\pi}_{0} \cos \theta \sin \theta d\phi d\theta \\ &= \int^{\frac{\pi}{2}}_{0} 2\pi \cos \theta \sin \theta d\theta \\ &= 2\pi \int^{\frac{\pi}{2}}_{0} \sin \theta \left( \sin \theta \right)' d\theta \\ &= 2\pi \left[ \frac{1}{2} \sin^{2} \theta \right]^{\frac{\pi}{2}}_{0} \\ &= \frac{2\pi}{2} \left( 1^2-0^2 \right) \\ &= \pi \end{align}$

2018-07-05

レンダラー開発のための測光学覚書Vol.3　ランバート反射BRDF

レン覚レンダリング物理数学

　レン覚（レンダラー開発のための測光学覚書）です！前回の投稿からだいぶ時間がたってしまったこともあり、自分でも記事を読み返したり、勉強しなおしたりしてました。
そして、とうとうレンダラーの開発をはじめたので、備忘録として学んだことをどんどん投稿しようと思います。今回は前回説明した「BRDF」について理解を深めていこうと思います。読みきりサイズなので、是非最後までお付き合いください。

ランバート反射について
ランバート反射のBRDFを求める
おわりに
- 参考
- 7/5追記

ランバート反射について

　さて、今回のテーマとなっている「ランバート反射」とは何かについて、最初に説明しようと思います。ランバート反射は拡散反射の一種で、いうなれば「理想的な拡散反射」です。どういう意味かというと、

光の入射角度にかかわらず、出射光は全ての方向に均一に反射されます。反射面の見た目の明るさ(輝度)はどの方向から見ても一定です。
http://www.systems-eng.co.jp/column/column03.html

らしいです。放射輝度の分布を図で示すとこんな感じです。
f:id:drumath:20180704210330p:plain

ランバート反射のBRDFを求める

　さて本題です。ここで導出に必要な物理量をしたの表のように定めます。

物理量	記号
放射束	$\Phi$
放射照度	$E$
放射輝度	$L$
反射率	$\rho$
立体角	$\omega$
BRDF	$f_{r}$
面積	$A$

シチュエーションによって、添え字に $i$ (入射)や $r$ (反射)をつけることがあります。

まず、反射率 $\rho$ を定義します。反射率は、

$\displaystyle \rho = \frac{d\Phi_{r}}{d\Phi_{i}}$

と定義されます。入射する光のエネルギーと反射する光のエネルギーの比ということで、イメージはしやすいですね。
さて、この反射率の定義に沿ってBRDFを導出したいのですが、そのためには放射束から放射輝度まで次元を落としていく必要があります。

入射放射束を変形する

まずは入射放射束を変形します。とはいえ放射束の定義に従って

$\displaystyle \begin{align} \Phi_{i} &= \int_{A}\int_{\Omega} \left( \omega' \cdot n \right)L_{i} \left( x, \omega' \right)d\omega'dA \\ &= \int_{A}E(x)dA \\ d\Phi_{i} &= E(x)dA \end{align}$

反射放射束の変形

　次に反射放射束を変形していきます。同じように定義から攻めていくと

$\displaystyle \begin{align} \Phi_{r} &= \int_{A}\int_{\Omega} \left( \omega \cdot n \right)L_{i} \left( x, \omega \right)d\omega'dA \end{align}$

ここで、ランバート反射した放射束は立体角によらずに一定なので

$\displaystyle \begin{align} \Phi_{r} &= \int_{A}L_{r} \left( x, \omega \right)\int_{\Omega} \left( \omega \cdot n \right)d\omega dA \\ d\Phi_{r} &= L_{r} \left( x \right) dA \int_{\Omega} \left( \omega \cdot n \right)d\omega \end{align}$

また、レンダリング方程式を参考にして

$\displaystyle \begin{align} L_{r}(x) = \int_{\Omega} \int_{A} f_{r}(x, \omega, \omega') \left( \omega \cdot n \right) L_{i}(x)dAd\omega \end{align}$

ここでも $f_{r}$ や $L(x)$ は立体角に依存しないので、

$\displaystyle \begin{align} L_{r}(x) &= f_{r,d}(x) \int_{\Omega} E_{i}(x) d\omega \\ &= f_{r,d}(x)E(x) \end{align}$

となるので、

$\displaystyle \begin{align} d\Phi_{r} = f_{r,d}E(x)dA\int_{\Omega}(\omega \cdot n)d\omega \end{align}$

反射率からBRDFを求める

　さて、ここまで来たので簡単なのですが

$\displaystyle \begin{align} \rho &= \frac{d\Phi_{r}}{d\Phi_{i}} \\ &= \frac{f_{r,d}E(x)dA\int_{\Omega}(\omega \cdot n)d\omega}{E(x)dA} \\ &= f_{r,d}\int_{\Omega}(\omega \cdot n)d\omega \end{align}$

ここで $\omega, n$ は正規化されているので、

$\displaystyle \begin{align} \int_{\Omega}\cos \theta d\omega &= \int^{\frac{\pi}{2}}_{0}\int^{2\pi}_{0}cos \theta \sin \theta d\phi d \theta \\ &= \pi \end{align}$

drumath.hatenablog.com

となるので、

$\displaystyle \begin{align} f_{r,d}(x) = \frac{\rho}{\pi} \end{align}$

が導けました。

おわりに

全休の日を利用して書きましたが、復習の時間が多くて結局夜になってしまいました...眠い。あれ、明日1限あったようなきがs
最後まで読んでいただき、ありがとうございました。

参考

qiita.com

7/5追記

$\int_{\Omega} \cos \theta d\omega$ の途中式が間違っていたので訂正しました。