レンダラー開発のための測光学覚書Vol.2 レイトレースのための基本的な物理量からレンダリング方程式まで
どうも、前回に引き続き、『レンダラー開発のための測光学覚書』シリーズ第2弾です。前回は立体角についての数学の話だったので、今回からは物理の話に入っていきましょう。
基本的な物理量
放射束
光とは粒子であり、波である。これが今の物理の定説です。しかし未だに謎が多く、光とは何かというのは完璧に答えることはできません。しかし、光は私たちに世界を知覚させることができる、とても身近な存在ですよね。ゆえに経験からいろんなことがわかります。例えば、虫眼鏡で黒い紙に光を1点に集中させれば火が出るように、光はエネルギーを持っています。ここで紹介する「放射束」は単位時間あたりの光のエネルギーという定義で、測光の分野では最も基本的な物理量です。
放射照度
単位面積当たりの放射束を放射照度といいます。
放射強度
ここで、前回の内容である、立体角の概念を導入します。ラジアンの立体版でしたね。忘れてしまった方はこちらをどうぞ。
drumath.hatenablog.com
放射強度は単位立体角当たりの放射束として与えられる物理量です。
放射輝度
放射輝度は、単位投影面積、単位立体角あたりの放射束として定義されます。先に式を出すと、
例えば、下の図のように、光が地面に向かって
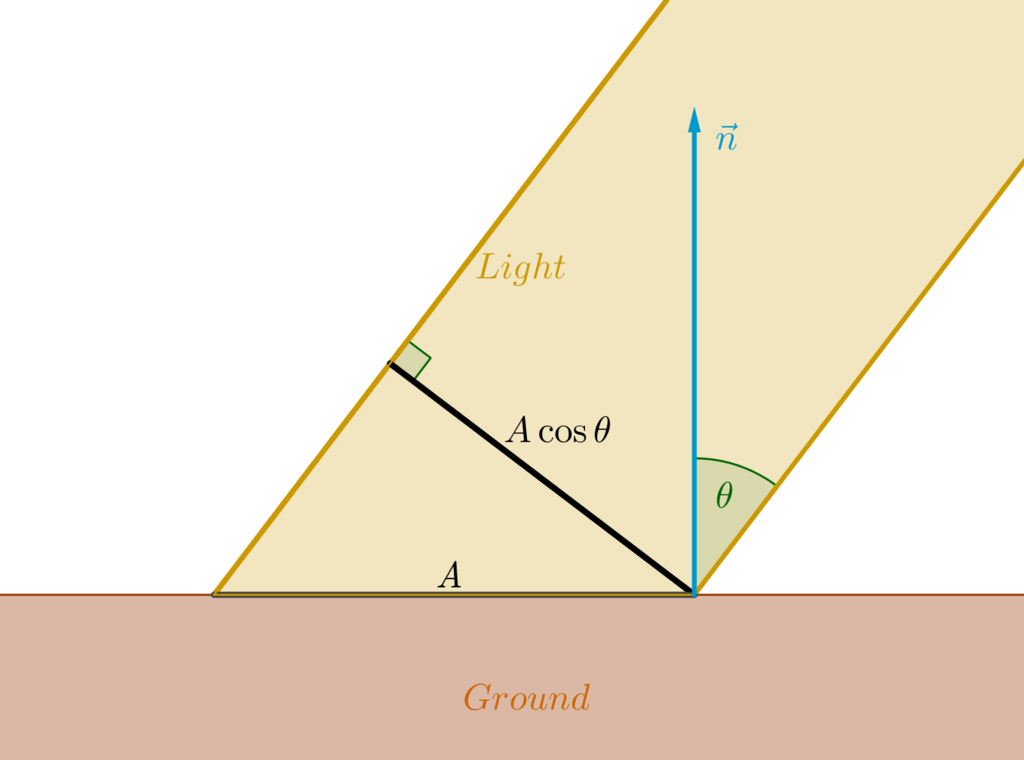
このとき、光が当たっている面積を
ここで、光の進行方向に垂直な面を考えます。すると、その面と光が当たっている面積は、図に示した通り、
放射輝度は積分すれば、いろんな物理量が導けるので、シミュレーションでは大変重宝します。例えば放射束を出したい時には
マテリアルの決定
ここまで光について見てきました。ここでは実際にレンダリングするとき、もう一つ重要な「どんな材質に光が当たったか」を決めるための関数をご紹介します。
BSSRDF(英:bidirectional scattering surface reflectance distribution function、日:双方向散乱面反射率分布関数)
光が物質の表面に当たったら、入射角と同じ大きさの反射角で反射し、屈折の法則に従って屈折することは高校生、いや中学生で習いました。しかし現実はそんなに甘くありません。なぜなら完全に平らな面など存在しないからです。実際にはすごく小さな凸凹があって、その凸凹に当たって光はあらゆる方向に反射していきます。これを散乱というのでしたね。また、光はどの物質でも通過します。つまり物質の表面で屈折した光はそのうち物質中で反射して出てくるかもしれないし、反射を繰り返して物質を通過するかもしれないのです。このように物質を通過した光が反射して出ていくことを「表面下散乱」といいます。このように表面化散乱の様子を示す関数が、BSSRDFと呼ばれる関数です。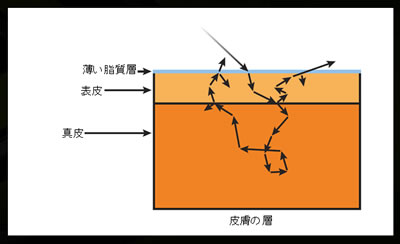
BRDF(英:bidirectional reflectance distribution function、日:双方向反射率分布関数)
BRDFはBSSRDFを簡略化したモデルです。正確に言うと、BSSRDFの簡略版は、BRDFとBTDFを足しあさせたBSDFというモデルなのですが、拡散反射や鏡面反射だけのモデルの場合、BRDFで事足りるということなんだと思います。BRDFは入射位置からでる反射光をモデル化したもので、先ほどの表面下散乱を考えないもので、入射光による放射照度と反射光による放射輝度の比で与えられます。
ここで、式の中の物理量に以下のものを使います。(なんか今更な感じもしますが)
| 物理量 | 意味 |
|---|---|
| 放射束 | |
| 放射照度 | |
| 放射輝度 | |
| BRDF | |
| 入射角 | |
| 入射光、及び反射光の方向 | |
| 入射面に対する法線 |
添え字のや
はそれぞれ入射光関係(incidence)、反射光関係(reflectance)という意味です。
BRDFの意味(高校生なりの解釈)
私は最初BRDFの式を見て、なんでこうなるんだかわかりませんでしたw というのも、なぜ放射照度と放射輝度という二つの違う量の比で表すのかが意味不明でした。しかもこんなに複雑な式で、さも微積させる気しかないような雰囲気ですよね。頭の中ではグラサンかけてる厳ついおっさんが突然出てきたみたいなイメージでした。絡みづらいわ。
しかし、BRDFもこんな風に変形すれば、目的は一目瞭然です。
このようにすると、後述するレンダリング方程式とほぼ形は一緒です。つまり、いま私たちが求めたいのは放射輝度である。前述のとおり放射輝度さえわかればほかの物理量は積分すれば求まりますからね。だから普通はBRDFを求めよう、なんてことはしないんじゃないかな。
もう一回式(1)を見てみましょう。
半球で積分をしている意味は、面に対して、あらゆる方向から入射してくる光の和という意味ですね。このおかげで、グローバルイルミネーションが実現できます。
レンダリング方程式
さて、ついにレンダリング方程式です。とはいえ、先ほどの内容がわかっていれば余裕です。ようは出ていく放射輝度を求める方程式です。
出射する光というのは、表面から放射される光と反射される光の和で求まります。これは感覚的ですね。つまり、
| 反射光(reflected)の放射輝度 | |
| 放射光(emitted)の放射輝度 | |
| 出射光(outgoing)の放射輝度 |
とすれば、求めるは
最後に
ここまで学習するのにはとても時間がかかりました。しかし、レンダリングの原理が少しわかったような気がして、自信が付きました。既存のレンダラーなど見ていると、いつもは何気なく見ている言葉も、「これ知ってる!」ってなってなんだか楽しいですw BlenderのCyclesレンダラーも、マテリアルの名前は「~~BSDF」という風になってますけど、材質決定の関数だなんて思いませんでした。これからも頻度は高くないかもしれないけど、このシリーズは続けていこうと思います。最後まで見てくださり、ありがとうございました。
参考文献
qiita.com
↑いつもお世話になっています。より詳しい内容が知りたい方はこのリンクへ飛んでみてください。
raytracing.hatenablog.com
↑教育用のレンダラーを作ってくださっています。日本語のコメントがあるって素敵
qiita.com
↑こちらもわかりやすく解説してくださっています。
Blenderで水の中の表現
どうも、今回はYafarayレンダラーを使って海の中を作ってみます。あまり長くはならないと思うのでお付き合いください。
海のオブジェクトとその他の環境を作る
では早速作っていきます。まず、画面に平面のオブジェクトを作成し、「海洋モディファイア」を付与します。
すると、こんな感じになります。
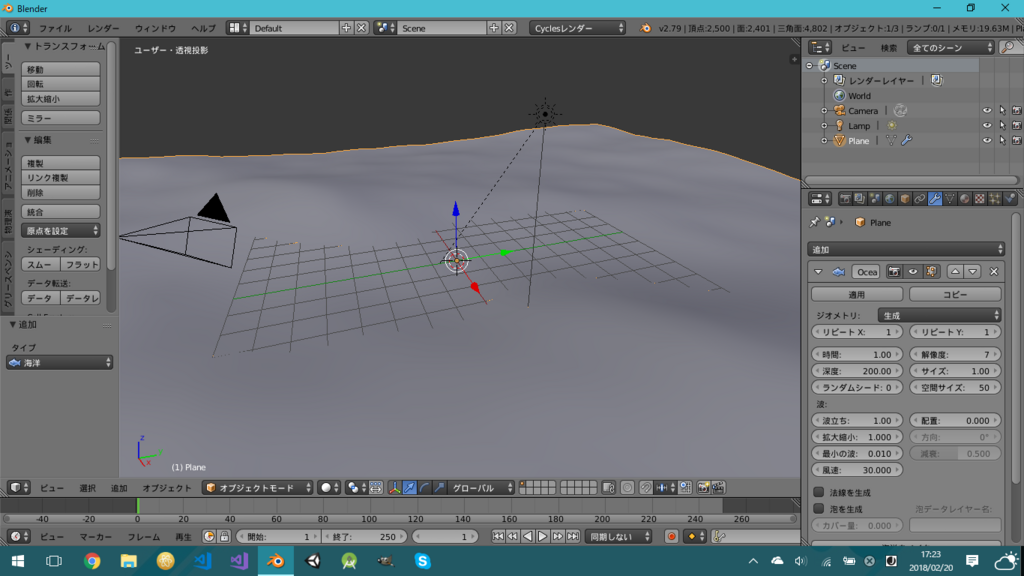
そして海洋を囲むように空間を作ります。
私は上面を除去したCubeオブジェクトに「厚み付けモディファイア」を付与しました。別に上面が閉じていてもいいのですが、Lampでサンを使いたいので私は開けました。
今の画面はこんな感じ。中にカメラも入れてください。
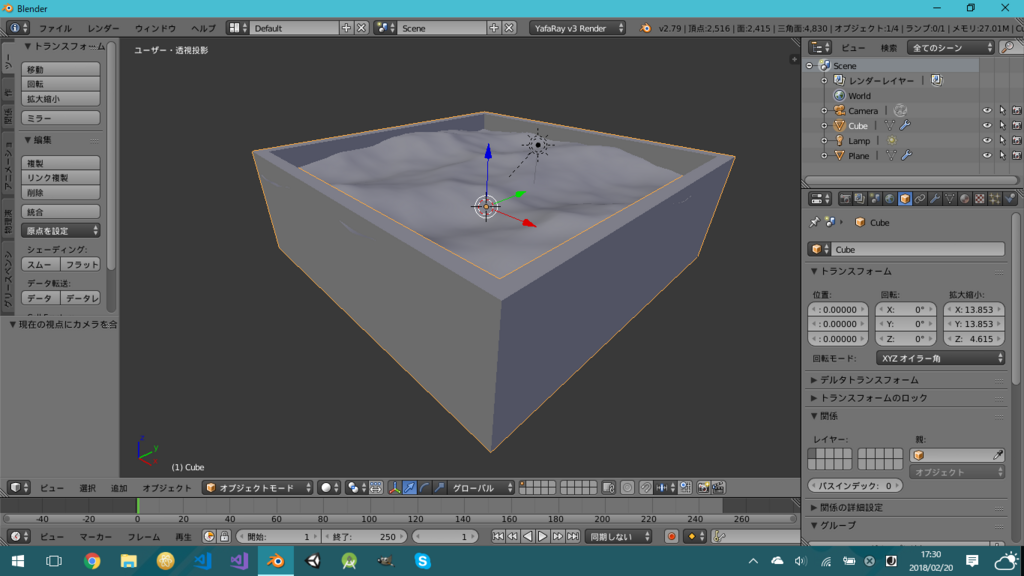
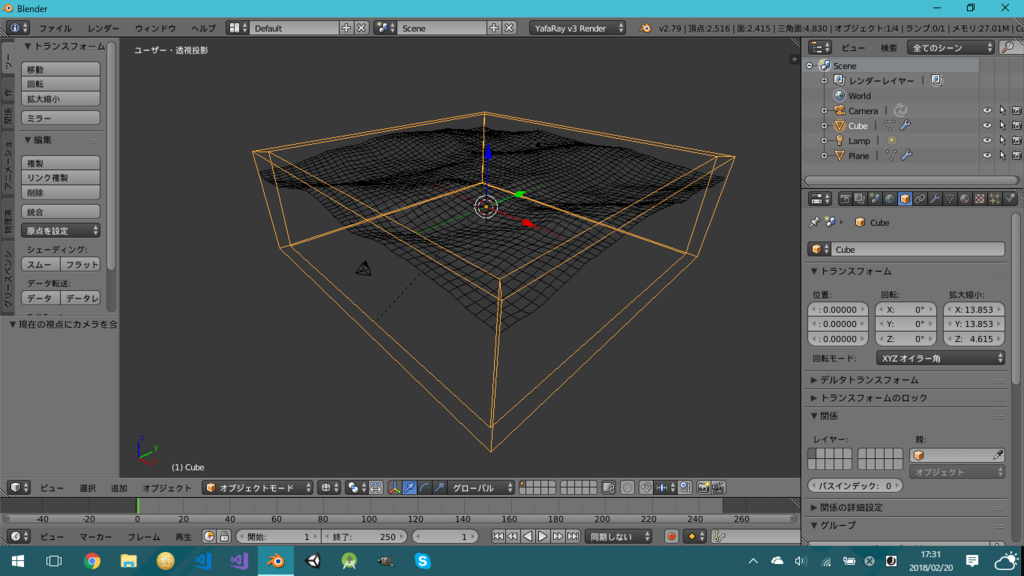
海洋の設定
先ほど追加した「海洋もモディファイア」ですが、私の設定はこんな感じ
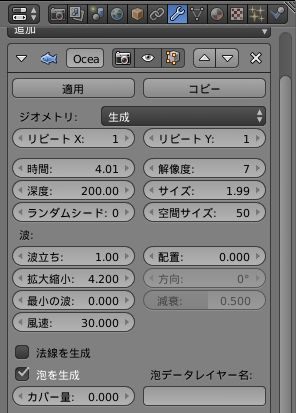
時間を変えると波が変化するので、いい感じの時間を選んでください。イイ感じの時間とは、波がまぁまぁ立っているときですかね。波がないと、海洋独特のコースティクスが生まれませんので。
マテリアルも編集していきます。
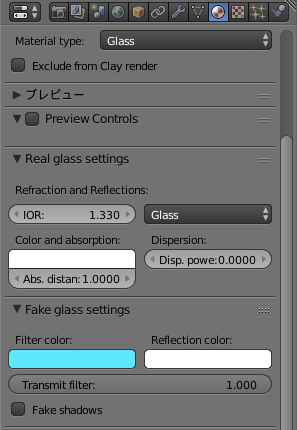
IOR(屈折率)は水の値を設定しました。
レンダリングしてみる
ではフォトンマッピングでレンダリングします。主要な設定は以下の通り。
| 名前 | 値 |
|---|---|
| Lighting Method | Photon Mapping |
| 深度 | 16 |
| バウンス | 9 |
| サンプル | 16 |

海洋モディファイアの解像度の値を7→10に変えてみましょう。

おわりに
今回はすごく早く書き終わりましたw とはいえCyclesでの再現で困っていたのでYafarayでできてよかったです。これからもYafarayの記事を書くかもしれないのでよろしくお願いします。
Yafarayについての他の記事↓
drumath.hatenablog.com
追記(2018/3/2)
動画で作ってみました。コンポジットし忘れたので、AviUtlでグロー効果をかけました。
youtu.be
レンダラー開発のための測光学覚書Vol.1 立体角について
どうも。大学生の勉強の予習になればと、レンダラー制作に向けて少しずつ勉強を始めている、drumathです。実際わからないことだらけなので、『レンダラー開発のための測光学覚書』というシリーズで、学習してきたことを整理していきたいと思います。もしよろしければ、解釈や式の導出などが間違っていた場合に教えていただけるとありがたいです。
今回は本格的に光学の分野には触れませんが、物理量の基本となる立体角についてまとめていきます。
立体角とは?
ラジアンの定義を振り返る
高校になっていきなり導入された弧度法ですが、なぜとなるのか、説明できますか?「簡単だよ!」という方は飛ばしていただいて構いません。
弧度法の定義はで、
は弧度法での角度、単位はラジアンです。
は
での弧の長さ。
は半径です。つまり、円周の長さと半径の比であらわされる値なのです。とても直観的だと思いませんか?対して度数法の場合、一周を360個に分けた内、どれくらいを占めるかという、とてもあいまいな値です。一周が360°なんて一体だれが考えたのでしょうか。古代文明の60進法からですよね、たぶん。
数学Ⅲを習うと、弧度法を使うメリットがわかります。詳しくはほかの記事に書いてあることを参照してほしいのですが、のような三角関数の微分は弧度法を使うことによって、きれいな形で表されます。個人的な解釈なのですが、三角関数自体、直角三角形の辺の比で表される関数なので、弧と半径の比という定義はなじみやすいのではないかと考えます。
微小立体角を求める
設定
光の物理量は微分と積分のオンパレードです。ですので、ここで微小立体角、を決めたいと思います。まず先ほどの画像の領域について、横が
、縦が
の微小長方形で、立体角が
と定めます。
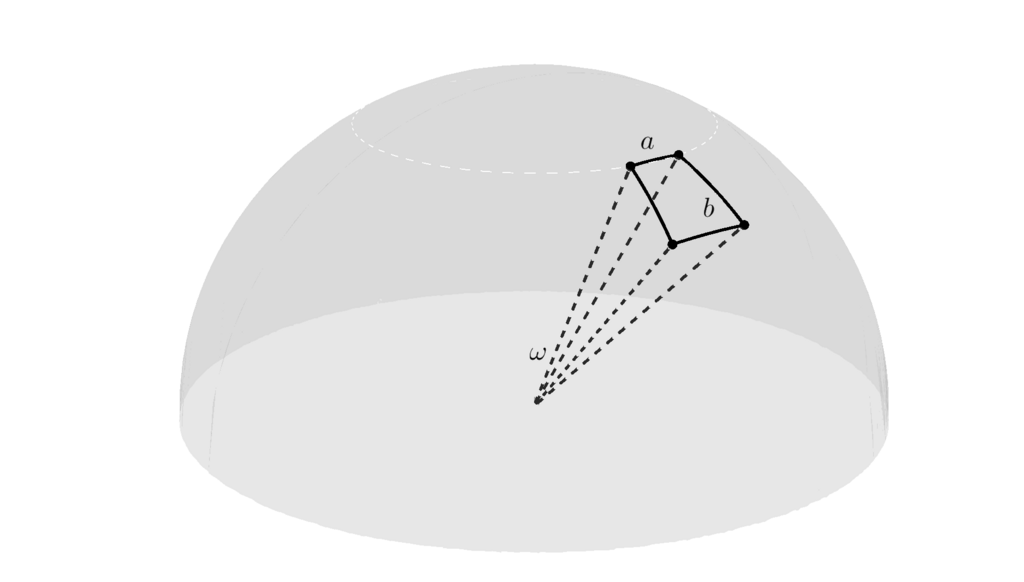
当然、
微分だ!
さて、では、
が微小な量だとします。そうすると立体角
も微小な量になり、長方形領域は点のように小さくなります。ここで領域の方向を以下のように定めます。
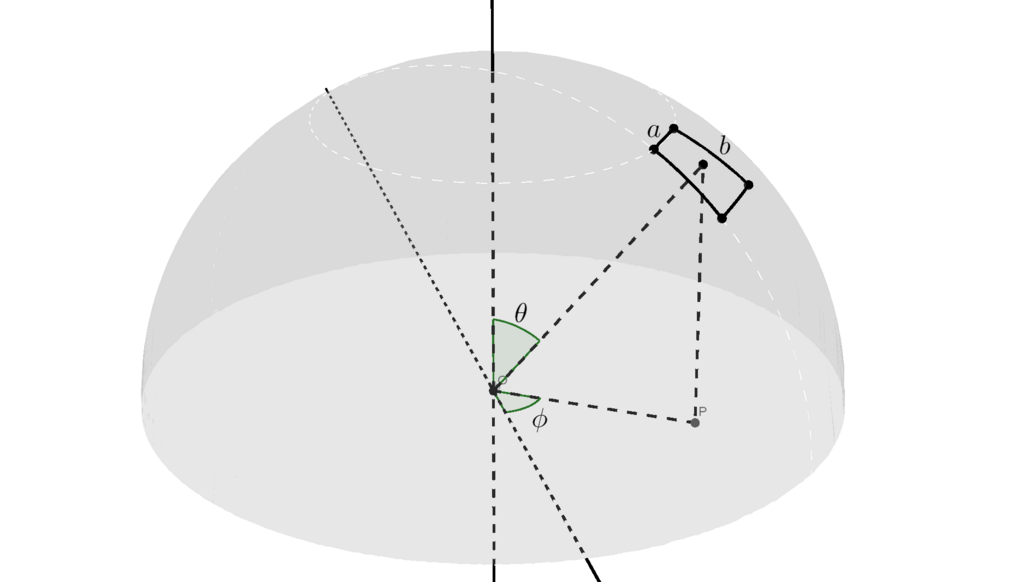
ではまず微小について考えましょう。長さ
である横の辺を含む円周の長さは弧度法の定義から求めることができるでしょう。弧度法での円周の長さ
は
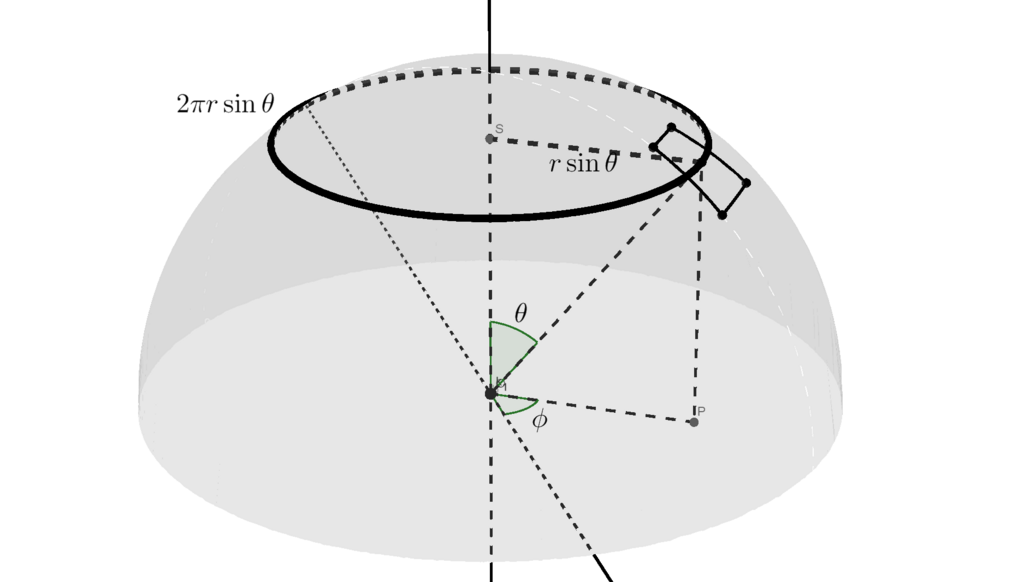
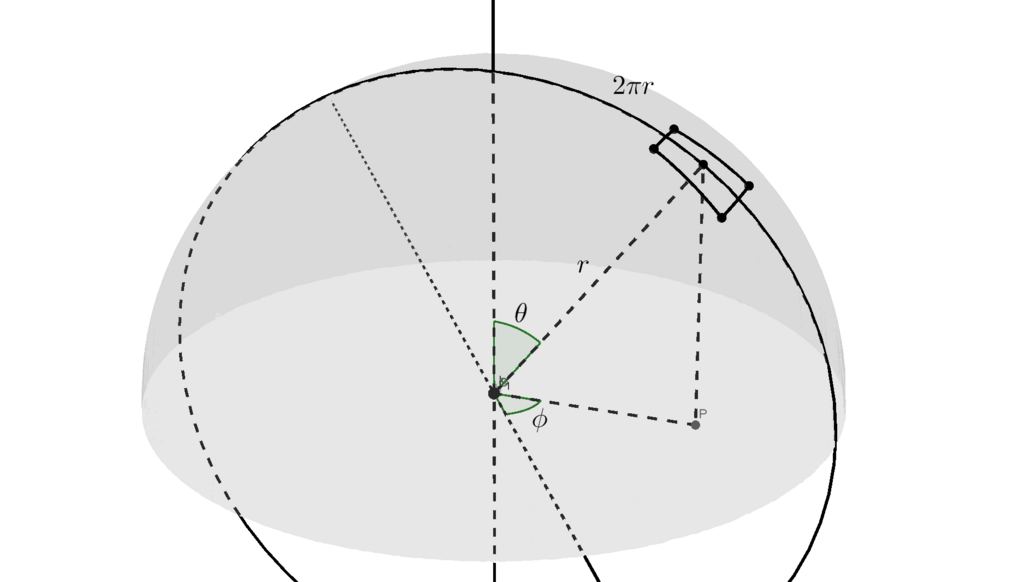
では、なぜ円周の長さは
すみません、たぶんもっとうまい説明があるし、なにしろすごく遠回りな考えなのはわかっていますが、私が思考した結果がこれなのです。引き続き
さて、続きを見ていきましょう。長さ
終わりに
今回は以上になります。立体角の概念は光学において基本的なものになりますが、私は学習当初あまりイメージできなかったので、数学Ⅲを習っている高校生にわかるように記事を書いたつもりです。最後まで読んでいただき。ありがとうございました。
参考文献
OpenGLでobjファイルの3Dデータを表示してみる
こんにちは。今回は入門したてのOpenGLでBlender出力のobjファイルビューワを作りたいと思います!
作るものについて
今回は下の画像のような3Dビューワを作ります。↓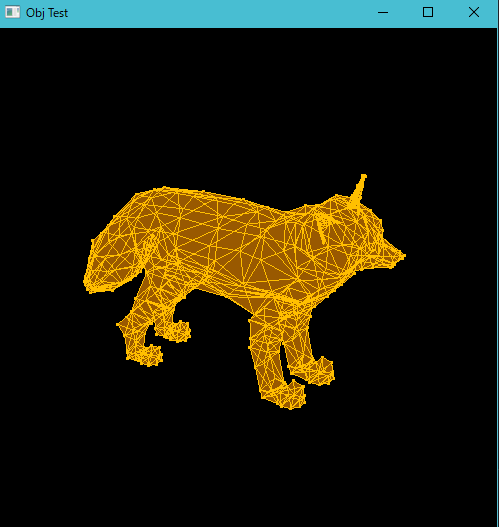
実装プラン
OpenGLをメインのライブラリとして使っていきますが、objファイル解析をRubyで実装しようと思います。その理由は、単純にRubyのほうがC++よりも文字列の処理がやりやすいからです。本当はオールC++でも全然できると思いますが、私が純粋なルビイストということもあり、Rubyを使用します。つまり、
という流れで実行していきます。また、objファイルはBlenderによって出力された3Dモデルデータを使用します。
開発環境など
使用する環境はこちらです。
| 項目 | 内容 |
|---|---|
| OS | Windows10 |
| ライブラリなど | OpenGL、freeglut |
| コンパイラ | Ruby2.2.4p230、bcc32 |
| エディタ | Visual Studio Code 1.19.3 |
| Blenderバージョン | Blender2.79 |
いざ、Rubyサイドを実装だ
Blenderでobjファイルにエクスポート
例えば、BlenderでCubeを追加したときのデフォルトのオブジェクトをobjファイル出力してみましょう。
まず、[ファイル]→[エクスポート]→[Wavefront(.obj)]とクリックしていきます。そうすると、下の画面のようになります。

普通にエクスポートボタンを押したくなると思いますが、ここで「三角面化」を忘れないでください!今回は面が三角形であることを前提に頂点を結んでいきます。もし多角形の面があったらちょっと厄介なことになりますので、必ず設定してください。
objファイルの形式を知る
先ほどの要領でobjファイルをエクスポートすると、このような内容が吐き出されます。
# Blender v2.79 (sub 0) OBJ File: '' # www.blender.org mtllib cube_obj_test.mtl o Cube_Cube.001 v -1.000000 -1.000000 1.000000 v -1.000000 1.000000 1.000000 v -1.000000 -1.000000 -1.000000 v -1.000000 1.000000 -1.000000 v 1.000000 -1.000000 1.000000 v 1.000000 1.000000 1.000000 v 1.000000 -1.000000 -1.000000 v 1.000000 1.000000 -1.000000 vn -1.0000 0.0000 0.0000 vn 0.0000 0.0000 -1.0000 vn 1.0000 0.0000 0.0000 vn 0.0000 0.0000 1.0000 vn 0.0000 -1.0000 0.0000 vn 0.0000 1.0000 0.0000 usemtl None s off f 2//1 3//1 1//1 f 4//2 7//2 3//2 f 8//3 5//3 7//3 f 6//4 1//4 5//4 f 7//5 1//5 3//5 f 4//6 6//6 8//6 f 2//1 4//1 3//1 f 4//2 8//2 7//2 f 8//3 6//3 5//3 f 6//4 2//4 1//4 f 7//5 5//5 1//5 f 4//6 2//6 6//6
これは何を示しているのでしょうか。
まず、
v -1.000000 -1.000000 1.000000
のような「v ~」ではじまる行は、頂点の座標を記録しています。Vはおそらく頂点の英語Vertexを意味しています。「v」につづく小数が左からx,y,z座標を表わしています。
そして、
f 2//1 3//1 1//1
のように「f~」ではじまる行は面のデータを記録しています。「f」のあとに「2//1」のような数字をスラッシュで区切ったような記述がみられますが、それは「頂点/テクスチャ座標/法線ベクトル」というデータを表わしています。今回使うのはい一つ目の数字だけですので、あとは無視してください。この1つ目の数字は、どの頂点を使うかを示しています。つまり「2//1」だった場合、一番左の「2」という数が、「2番目の頂点を使うぞ」と言っています。何番目の頂点かは「v」から始まる行の上から何番目かで決まります。
面の情報はどの三つの頂点を使うかを表しています。つまり
f 2//1 3//1 1//1
ならば、この面は2番目の頂点と3番目の頂点と1番目の頂点で構成されていることを示します。
Rubyでobjファイルコンバータを作る
Rubyでは、objファイルを読み込み、あとでC++側でscanfするだけで簡単にデータが格納できるようなファイルを新たに作ります。というわけでコードはこんな感じ。
# vars vertex = [] face = [] # const regexp Face_regexp = /^f (\d+)\/\d*\/\d* (\d+)\/\d*\/\d* (\d+)\/\d*\/\d*/ Vertex_regexp = /^v (.*) (.*) (.*)/ # conversion obj file File.open(ARGV[0], 'r') do |file| file.read.split("\n").each do |line| if line =~ Face_regexp face << [$1, $2, $3].map { |m| m.to_i - 1 } elsif line =~ Vertex_regexp vertex << [$1, $2, $3].map(&:to_f) end end end # output vertex data File.open('vData.txt', 'w') do |file| vertex.each do |e| file.puts e.join(', ') end end # output face data File.open('fData.txt', 'w') do |file| face.each do |e| file.puts e.join(', ') end end
たとえば、さきほどの立方体のデータを読み込むと、
ruby obj_convert.rb cube.obj
vData.txtとfData.txtという二つのファイルが作成され、vData.txtには、
-1.0, -1.0, 1.0 -1.0, 1.0, 1.0 -1.0, -1.0, -1.0 -1.0, 1.0, -1.0 1.0, -1.0, 1.0 1.0, 1.0, 1.0 1.0, -1.0, -1.0 1.0, 1.0, -1.0
fData.txtには、
1, 2, 0 3, 6, 2 7, 4, 6 5, 0, 4 6, 0, 2 3, 5, 7 1, 3, 2 3, 7, 6 7, 5, 4 5, 1, 0 6, 4, 0 3, 1, 5
という内容が出力されていることがわかります。vDataのほうは、単純に座標のリストです。fDataのほうは、三角面を構成する座標のインデックスを表わしていますが、実際コードを見るとわかりますが、インデックスを-1しています。それは、objファイルは上から1,2,3...と数えますが、C++の配列では0,1,2...と数えるので、C++の仕様に合わせるためです。
いざ、OpenGLで描画
ファイル階層
ファイル階層はこんな感じになります。
ObjTest.cppを書いていく
最初にコードを出します。私はこんな感じで書きました。
#include <windows.h> #include <stdio.h> #include "GL\freeglut.h" #pragma comment (lib, "lib\x86\freeglut.lib") #define ARRAY_MAX 10000000 float vertex[ARRAY_MAX]; int lines[ARRAY_MAX]; int vertexDataSize=0, lineDataSize=0; void disp() { glClearColor(0,0,0,1); glClear(GL_COLOR_BUFFER_BIT); glEnableClientState(GL_VERTEX_ARRAY); glVertexPointer(3,GL_FLOAT,0,vertex); // 頂点の描画 glPointSize(3); glBegin(GL_POINTS); { for(int i=0;i<vertexDataSize;i++) glArrayElement(i); } glEnd(); glColor3f(0.6,0.35,0); glBegin(GL_TRIANGLES); { for(int i=0;i<lineDataSize;i++){ glArrayElement(lines[i*3]); glArrayElement(lines[i*3+1]); glArrayElement(lines[i*3+2]); } } glEnd(); glColor3f(1.0,0.75,0); glBegin(GL_LINES); { for(int i=0;i<lineDataSize;i++){ glArrayElement(lines[i*3]); glArrayElement(lines[i*3+1]); glArrayElement(lines[i*3+1]); glArrayElement(lines[i*3+2]); glArrayElement(lines[i*3+2]); glArrayElement(lines[i*3]); } } glEnd(); glFlush(); } void timer(int x) { glRotatef(1,0,1.0,0); glutPostRedisplay(); glutTimerFunc(50,timer,0); } void InitialProc() { FILE *fpVData, *fpFData; fpVData = fopen("vData.txt","r"); fpFData = fopen("fData.txt", "r"); if((fpVData==NULL)||(fpFData==NULL)){ printf("file error!!\n"); return; } while (fscanf(fpVData,"%f, %f, %f",&vertex[vertexDataSize*3],&vertex[vertexDataSize*3+1],&vertex[vertexDataSize*3+2])!=EOF) vertexDataSize+=1; while(fscanf(fpFData,"%d, %d, %d",&lines[lineDataSize*3],&lines[lineDataSize*3+1],&lines[lineDataSize*3+2])!=EOF) lineDataSize+=1; } int main(int argc, char **argv) { InitialProc(); glutInit(&argc, argv); glutInitWindowPosition(50,100); glutInitWindowSize(500,500); glutInitDisplayMode(GLUT_SINGLE|GLUT_RGBA); glutCreateWindow("Obj Test"); glRotatef(30,1.0,0,0); glRotatef(30,0,1.0,0); glScalef(0.8,0.8,0.8); glutDisplayFunc(disp); glutTimerFunc(100,timer,0); glutMainLoop(); return 0; }
InitialProc()関数内ではvData.txtとfData.txtからデータを入力して配列に格納しています。こうすることで、あとでglArrayElementsで簡単に頂点を描画したり、辺を作ったりすることができます。
また、timer()関数で0.05秒ごとに回転させています。
【自己紹介もかねて】Yafarayでコースティクスと光の分散(dispersion)をレンダリングしてみる
初めまして。初投稿になります、drumathです。タイトルにある通り、自己紹介もかねまして、先日Blenderに導入したYafarayレンダラーについて少し記事を書こうと思います。
自己紹介
PCいじりが好きな高校生です。最近はOpenGLで3Dソフトを作っていて、前はXamarinでスマホアプリを作ったり、Unityでゲームを作ったりしていました。どれも中途半端に初心者なのでどれか一つに絞って極めたい!と思いつつ、ほかの方面にも興味が出てしまう、なんていう贅沢な悩みを抱えています。他にも3DCGをやったり、アコギを弾いたり、ドラムを叩いたり、クトルゥフTRPGをやったり・・・と飽きっぽい性格なので趣味がどんどん増えていきます。はてなブログはプログラミングするときにいつもお世話になっていたので、いつか自分でも書いてみたいなぁなんて思っていました。文才がないので、まとまりのない文章になってしまうかもしれませんが、ぜひ興味のある記事にはコメント、シェア等してくださるとありがたいです。これからどうぞよろしくお願いします。
最近のマイブーム「レンダリング」
前述したとおり飽きっぽい性格なので、マイブームはちょくちょく変わります。次の記事を書くころにはまた変わってしまっているかもしれませんし、この記事を書くきっかけにもなったことなので、少しご紹介します。
レンダリングとは、3Dで作られたオブジェクトを光の反射、屈折や陰影をコンピュータ内で計算、シミュレートし、2D画像に変換することを言います。3DCGの作品を作る時にはだいたいレンダリングし、ポストプロセス(コンポジットなど)を踏んで完成となります。レンダリングという作業は日常的にやっていたのですが、今使っているノートパソコンにグラボを積んでいないのでレンダリングはすべてCPUで行っている状態です。ゆえにレンダリング速度が遅くてあまり好きな作業ではありませんでした。
しかし、最近見た『宝石の国』というアニメを見て、その美麗なCGに感銘を受けました。正確に言うと、
主題歌いいなぁ→ほう、オールCGなのか→内容めっちゃいい→(『アニメCGの現場』をみて)制作陣天才かよ・・・
という具合に自分の創作意欲を掻き立てるような、新鮮な感覚でした。
こんなCGを作ってみたい!と思いました。宝石のようなモデルならBlenderで作り、Glass BSDFマテリアルで再現できます。ということでQiitaで記事を書きました。
Yafaray導入までの流れ
Qiita執筆時はよくできたと思ったのですが、本物の宝石とはちょっと違うなぁって感じがしました。そんな疑問は、前述した『アニメCGの現場』で解決しました。
自然の透明な材質に光が入るとその光は屈折し、ほかの表面に到達するときに特有の模様を描きます。これをコースティクスというのですが、BlenderのマニュアルによるとCyclesレンダラーはコースティクスをサポートしていない、というような記述が見れます。はて、どうしたものか。

「Blender コースティクス」みたいな感じで検索をかけると、それっぽい画像が出てきたり疑似的に再現していたりとデモはあるのですが、やはり新しいレンダラーを導入するのが得策だなと思い、Yafarayを導入することになりました。
導入方法は、まず下記のYafarayの公式サイトからYafarayレンダラーのソースなどが入った.zipファイルをダウンロードし、Blenderで「ファイル」→「ユーザー設定」→「アドオン」の画面の下にある「ファイルからアドオンをインストール」をクリックして先ほどDLしたzipファイルを指定すれば完了です。
レンダリングシステムについての話
レンダリングとは光の計算をして3DCGを2Dの作品に変換する処理だということは前に話しました。光の計算とはレンダリング方程式というものをコンピュータが解くことにより行われるのですが、その方式にはいくつか種類あります。有名なものとしては、
などがあります。
詳しい話は数学の知識が必要なのでしませんが、レイトレーシングは光源から出た光をカメラから逆にトレースすることで計算をします。逆に、フォトンマッピング方式は光源からの光線をカメラ、光線両方からトレースすることで大域証明(GI)やコースティクスを再現できます。まさに、フォトリアルな作品を作るにはもってこいのレンダリング方式です。また、透明な材質(例えばガラスや水)を通る光の屈折や散乱には適しているが、金属による鏡面反射は計算に時間がかかる、といった得意不得意があります。今回はコースティクスを再現したいので、Yafarayレンダラーでフォトンマッピング方式のレンダリングをしたいと思います。
シーンを作る
それではシーンを作っていきます。こんな感じ。↓

設定としてはまずCubeで空間を作って、なかをポイントライトで照らします。そしてそれとはまた別にスポットライトでダイヤモンドのマテリアルを持ったオブジェクトを照らしてコースティクスを作ります。

部屋の中とダイヤモンドのかけらのオブジェクトです。ダイヤモンドのマテリアルは下記のような設定で作りました。
IORには実際のダイヤモンドの屈折率を入力します。
次に空間を照らすポイントライトと、ダイヤモンドを照らすスポットライトの設定です。
ポイントライトの設定です。
スポットライトの設定です。
実際当てているスポットライトはめっちゃ明るいです。できるだけはっきりとコースティクスを描こうと思うのでこうしました。
さて、これでレンダリングしてみましょう。レンダリングの設定は以下の通りです。

見事にコースティクスが描かれていますね。ちなみに同じような設定でCyclesレンダラーでレンダリングすると、こうなります。

これでもサンプル数は4096なのですが、ノイズが走っていますね。この結果から、どうやらCyclesでもコースティクスは再現できるようですが、かなりのサンプル数が必要だということがわかります。もしこのノイズを消したい場合には、「間接値を制限」のところに「1.0」を入力すると消えますよ。
光の分散をレンダリング
さて、次は光の分散をレンダリングしましょう。といっても簡単で、先ほどのダイヤモンドのマテリアルの設定に「dispersion」という項目があるのですが、そこに任意の値を入れれば分散をシミュレートできるみたいです。下の画像は「0.3」を代入したものになります。

きれいですねぇ。宝石らしくなったのではないでしょうか。
まとめ
Yafarayレンダラーを使うことによりフォトリアルなレンダリングをすることができました。またCyclesよりもYafarayのほうがレンダリング時間もはるかに速いので、今後重宝したいと思います。
今回は以上になります。こんな感じの記事をたまに投稿しようと思うので、よろしくお願いします。
追記
アニメーションレンダリングしてみました。よかったら見てください。↓
